акордов метод
Итерационен метод
Методът на проста итерация за уравнениетоf(x) = 0 е както следва:
1) Оригиналното уравнение се трансформира във форма, удобна за повторения:
2) Изберете първоначалното приближениех0 и изчислете следващите приближения, като използвате итеративната формулаxk=φ(хk-1),k=1,2, . (2.3)
Ако има граница на итерационната последователност, , тя е коренът на уравнениетоf(x) = 0, т.е.f(ξ) =0.
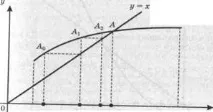
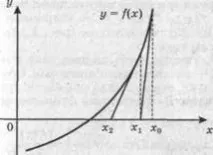
Ориз. 2.Сближаващ процес на итерации
На фиг. 2 показва процеса на получаване на следващото приближение с помощта на итерационния метод. Последователността от приближения се сближава към коренаξ.
Теоретичните основи за прилагане на итерационния метод са дадени от следната теорема.
Теорема 2.3. Нека са изпълнени следните условия:
1) коренът на уравнениетох=φ(х)принадлежи на отсечката [а,b];
3) има такова положително числоq k .(2.4)
Очевидно тази теорема поставя доста строги условия, които трябва да бъдат проверени преди прилагането на итерационния метод. Ако производната на функциятаφ(x) е по-голяма от единица по абсолютна стойност, тогава итерационният процес се разминава (фиг. 3).
y=φ(x)y=x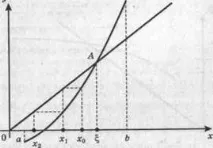 |
Ориз. 3.Разминаващ се процес на итерации
Неравенството
Методът на хордата се състои в замяна на криватаy=f(x) с права линия, минаваща през точките (а,f(a)) и (b,f(b)) фиг. 4). Като следващо приближение се приема абсцисата на пресечната точка на правата с остаOX.
За да получите изчислителната формула на методахорди, записваме уравнението на права линия, минаваща през точките (a,f(a)) и (b,f(b)) и приравнявайкиyна нула, намирамех:
Þ
Алгоритъм на акордния метод :
2) изчислете следващия номер на итерация:k=k+ 1.
Нека намерим следващотоk-e приближение по формулата:
3) акоf(xk)= 0 (коренът е намерен), тогава преминете към стъпка 5.
5) изведете стойността на коренаxk;
Забележка. Действията на третия параграф са подобни на действията на метода на половината разделяне. Въпреки това, при хордовия метод, един и същи край на сегмента (вдясно или вляво) може да бъде изместен на всяка стъпка, ако графиката на функцията в близост до корена е изпъкнала нагоре (фиг. 4,a) или вдлъбната надолу (фиг. 4,b). Следователно разликата на съседните приближения се използва в критерия за конвергенция.
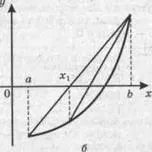 |
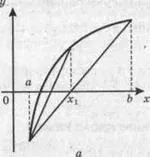
Ориз. 4.Метод на акордите
4. Метод на Нютон(тангенс)
Нека се намери приблизителната стойност на корена на уравнениетоf(x)= 0 и го означим схп.
Първият метод изразява геометричния смисъл наМетода на Нютони се състои в това, че вместо пресечната точка на графиката на функциятаy=f(x) с остаОxтърсим пресечната точка с остаОxна допирателната, начертана към графиката на функцията в точката (xn,f(xn)), както е показано на фиг. 5. Уравнението на допирателната има форматаy - f(xn)=f '(xn)(x-xn).
Ориз. 5.Метод на Нютон (тангенс)
В точката на пресичане на допирателната с остаOx, променливатаy= 0. Приравнявайкиyдо нула, изразявамеxи получаваме формулататангентен метод:
(2.6)
Вторият начин: разширяваме функциятаf(x) в ред на Тейлър в околността на точкатаx = xn:
Ограничаваме се до линейни членове по отношение на (х-хп), приравнявамеf(x) на нула и, изразявайки неизвестнотохот полученото уравнение, обозначавайки го схn+1, получаваме формула (2.6).
Нека представим достатъчни условия за сходимост на метода на Нютон.
Теорема 2.4. Нека на отсечката [а,b] са изпълнени следните условия:
2) производнитеf '(x) иf''(x) са различни от нула и запазват определени постоянни знаци;
3)f(a)× f(b)0, тогава итеративната последователност се сближава монотонно
Забележка. Имайте предвид, че методът на акордите просто идва от противоположната страна и двата метода могат да се допълват взаимно. Възможен е и комбинираниятметод на хорда-тангенси.
5.Секущи
Методът на секанса може да се получи от метода на Нютон чрез заместване на производната с приблизителен израз - формулата на разликата:
..
. (2,7)
Формулата (2.7) използва двете предишни приближенияxnиxn-1. Следователно, за дадено първоначално приближениеx0, е необходимо да се изчисли следващото приближениеx1,, например, като се използва методът на Нютон с приблизителна замяна на производната по формулата
,
Алгоритъм на втори метод:
1) зададени са начална стойностх0 и грешкаε. Изчислете
;