Анализ на динамичния механизъм
Работни страници





Съдържанието на произведението
3. ДИНАМИЧЕН АНАЛИЗ НА МЕХАНИЗМИТЕ
В резултат на динамичен анализ се намират истинските стойности на позициите, скоростите и ускоренията на всякакви точки на механизма, като се вземат предвид всички действащи сили.
3.1. Изграждане на параметри на динамичен модел.
Тъй като в реална машина всички движещи се връзки са свързани помежду си чрез кинематични двойки, тогава, знаейки закона за движение на една връзка (обобщена координата), можете да намерите законите за движение на останалите.
За да изградим динамичен модел на механизма, избираме първоначалната връзка 1 като редукционна връзка, към която привеждаме всички сили, действащи върху механизма, и инерционните моменти на движещите се връзки. Изследваният динамичен модел ще изглежда така (Фигура 3.1).

3.1.1 Намиране на намаления инерционен момент.
Редуцираният инерционен момент се определя по формулата, която има следния вид [3,4]:
, (3.1)
където n е броят на движещите се връзки, чиито маси и инерционни моменти са дадени; mi е масата на i-тата връзка; ISi е инерционният момент на i-тата връзка спрямо оста, минаваща през центъра на масата; S¢ix, S¢iy са проекции върху координатните оси на аналога на скоростта на центъра на масата на i-тата връзка; j¢i е аналог на ъгловата скорост на i-тата връзка.
За разглеждания механизъм на двуцилиндров кислороден компресор формулата (3.1) приема формата:
, (3.2)
Където
Диференцирайки израз (3.2) по отношение на обобщената координата j1, намираме производната на намаления инерционен момент:
(3.3)
Замествайки в (3.2) и (3.3) данните за механизма на четвърта позиция, намираме, че
Разглеждаме стойностите на Ip и за останалите позиции на механизма. Въвеждаме получените данни в таблица 4.1 и ги използваме за изграждане на графики на функцията Iп = f (j1) и (фиг. 3.2). Началото на координатите на графиката се поставя в началото на работния ход на механизма.
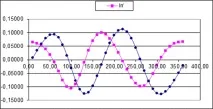
Ориз. 3.2. Диаграма на изменението на намаления инерционен момент и неговата производна.
3.1.2 Намиране на намаления момент.
Редуцираният съпротивителен момент се определя по формулата, която има следния вид [3,4]:
, (3.4)
където n е общият брой на движещите се връзки; m е броят на силите F, действащи върху i-тата връзка; Fix, Fiy - проекции на сила върху съответните координатни оси;l¢ix,l¢iy – проекции върху съответните координатни оси на скоростния аналог на точката на прилагане на силата; q е броят на моментите M, действащи на i-тата връзка.
За изследвания компресор формулата (3.4) приема съответно формата:
(3,5)
В тези формули F3y, F4y са проекциите върху оста y на силите на тежестта на връзки 3 и 4, които са съответно равни на:
3.2. Определяне на нарастването на кинетичната енергия на механизма
След като изградихме динамичен модел на изследвания механизъм, пристъпваме към неговия анализ. Ще анализираме динамичния модел с помощта на графично-аналитичния метод на Wittenbauer. За да изградите диаграма, трябва да знаете законите за промяна на намаления инерционен момент Ip и увеличението на кинетичната енергия T. Нека намерим закона за изменение на увеличението на кинетичната енергия.
Първо, в съответствие с (3.5) и таблица 3.1, начертаваме функцията Mps = f(j1). При нанасяне на графиката Mps = f(j1) поставяме координатната система в началото на работния ход на изследвания механизъм (фиг. 3.3). След това намираме работа Asнамален момент на съпротивителни сили Mps. Работата Ac се определя от численото интегриране на функцията Mps=f(j1). Интегрирането се извършва по метода на трапеца, според който
.
Тукj = 1,2,…е номерът на позицията на механизма, за която се изчислява работата в начална (нулева) позицияАс0 = 0. Стойностите на ъглитеj1jсе заместват в (3.6) в радиани.
СтойноститеАс, намерени по формула (3.6), се въвеждат в таблица 3.1 и по тях се изгражда графиката на функцията.
В стационарно състояние работатаАсна редуцирания момент на съпротивителните сили за цикъл е равна на работата на редуцираните движещи силиApd. Ако приемем, че задвижването развива постоянен намален момент на движещите силиMpd, намираме неговата стойност
-96.25/6.28=-15.326 Знакът минус в последния израз показва, че моментътMpdе насочен към преодоляване на намаления момент на съпротивителните силиMps. Изграждаме графика на функцията.
РаботатаАdна приведения момент на движещите силиMndсе изчислява по формулата
, (3.7)
къдетоj =1, 2…е номерът на позицията на механизма, за която се определя работатаAd. В начална (нулева) позицияAd=0.
Изчислени по формулата (3.7) стойности на работата на движещите силиAdвлизаме в таблица 3.1 и изграждаме графика на функцията върху тях (фиг.3.2).
Намираме закона за промяна в нарастването на кинетичната енергияDT, за което алгебрично добавяме произведениятаADиAc,
,