Атом на Зомерфелд

Теорията на Бор отразява правилно основните характеристики на спектралното поведение на водородния атом, но не може да обясни например фината структура на спектралните линии или тяхното разделяне, когато атомът е поставен във външно поле. Следващата стъпка в развитието на теорията на атома е направена от А. Зомерфелд, който предполага, че електрон във водороден атом може да се движи не само по кръгови, но и по елиптични орбити, за които също трябва да бъде изпълнено условието за квантуване на ъгловия момент, подобно на връзката (3.5). При това условие се оказа, че разрешените траектории на електроните са елипси с равни съответно голяма и малка полуос:

и

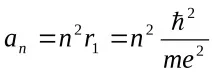
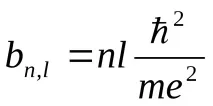
Тукn= 1, 2, 3. е основното квантово число,l= 1, 2, 3.n–е орбиталното квантово число. Енергиите на различните състояния се определят само от величината на голямата полуос на елипсата или главното квантово число:

, (3,8)

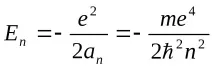
което в крайна сметка съвпада с (3.6). От друга страна, квантуваните стойности на ъгловия момент се определят от възможните стойности на квантовото числоl:

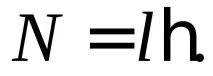
В развитието на идеите на Бор Зомерфелд разшири квантуването до ориентациите на орбитите на електроните в атома. Според идеята за „пространствено квантуване“,са възможни само такива ориентации на орбиталната равнина, при които проекцията на ъгловия импулс на електрона върху някаква избрана посокаzприема стойности, които са кратни на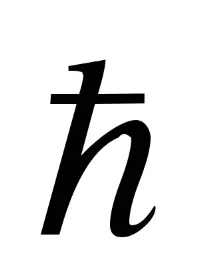

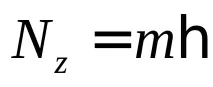
, т.е., къдетоm–е така нареченото магнитно квантово число, което може да вземе стойности, равни наm= 0, 1, 2,…, l.

Така състоянието на атома може да се характеризира с три квантови числаn,l,m, които определят възможните траектории на електрона и съответните физични величиниEn,N,Nz.

Трябва да се отбележи, че теорията на Бор-Зоммерфелд даде възможност само качествено, но и количествено да се обяснят основните закономерности в атомните спектри, включително ефектите на Зееман и Старк. Но основният недостатък на тази теория беше нейната вътрешна непоследователност: тя не беше нито последователно класическа, нито последователно квантова. Според W. Bragg, "в тази теория трябва, така да се каже, да използваме класическите закони в понеделник, сряда и петък, и квантовите закони във вторник, четвъртък и събота."

Описанието на водородния атом, съвместимо с експеримента и свободно от противоречия, се оказа възможно само с помощта на идеите и апарата на квантовата механика.

Водороден атом в квантовата механика

Нека разгледаме накратко крайния резултат от квантовомеханичното описание на водородния атом. Тук състоянието на атома също се определя от три квантови числа: главнотоn, орбиталнотоlи магнитнотоm, които приемат малко по-различни стойности, а именно:

От една страна, тези квантови числа задават състоянието на електрона под формата на така наречената вълнова функция

, квадратът на модула на която определя вероятносттаdW, че частицата ще бъде открита в рамките на елементарния обемdV:

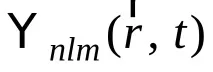
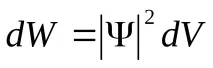
или, с други думи,

дава плътността на вероятността (вероятността за единица обем) за намиране на частица в дадено място в пространството, т.е.

.

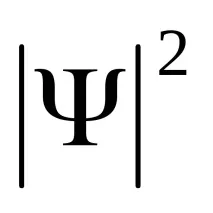
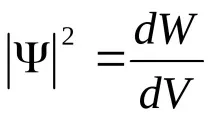
От друга страна, квантовите числаn,l,mопределят някои физически величини, характеризиращи състоянията на водородния атом. По този начин възможните стойности на енергията на атома се определят точно по същия начин, както в случая на модела на Бор-Зоммерфелд, а именно:

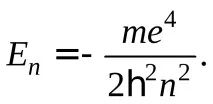
Ъглов момент и неговите проекциисе определят, както следва:

(3,9)

. (3.10)

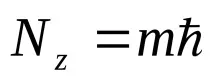
Външно представените резултати са подобни на резултатите от теорията на Зомерфелд.

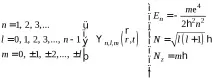
Възможните състояния на водородния атом (резултат от квантово-механично разглеждане) и спектроскопичните обозначения на състоянията са дадени на фиг. 3.3.

---