Целта на курсовата работа, Изходни данни - Изчисляване на плоски и пространствени конструкции

Целта на курсовата работа е да се развият уменията за изчисляване и изучаване на баланса на плоски шарнирни ферми.

Съдържанието на курсовата работа

Обектът на изследването е плоска шарнирна ферма, която представлява набор от прави пръти, свързани помежду си с идеални панти. Схеми на ферми и таблици с изходни данни са дадени в албума със задачи.

Параметрите, които трябва да бъдат зададени са:

геометрични характеристики на фермата;

плоска система от активни сили, приложени към възлите на фермата.

При съставянето на математическия модел се правят следните допускания:

прътите, образуващи фермата, са безтегловни, абсолютно твърди и прави;

свързващи панти - идеални (в тях няма триене).

1. Формирайте система от уравнения за определяне на реакциите на външните и вътрешните връзки.

2. Намерете стойностите на реакциите на външните и вътрешните връзки.

3. Извършете числен анализ на полученото решение за различни видове опори и тяхното разположение с помощта на компютър и изберете най-добрия вариант.

Работен ред

1. Изберете тяло (елемент) или система от тела със зададени действащи сили, чийто баланс ще се разглежда;

2. Използвайки аксиомата за освобождаване от връзки, считайте избраното тяло за свободно, заменяйки връзките, действащи върху него, с техните реакции;

3. Дайте анализ на получената система от сили, разберете статичната определимост на фермата;

4. Запишете условията на равновесие и съставете уравненията на равновесието:

използване на метода на рязане на възли;

5. Определете реакциите на външните и вътрешните връзки и проверете правилността на съставянето на уравненията на равновесието.

6. Провеждайте анализи и изследванияполучено решение:

да се изследва влиянието на вида на опорите и тяхното местоположение върху величината на реакциите на външните и вътрешните връзки.

изберете такова разположение на опорите, което осигурява минимален брой компресирани или опънати пръти (според указанията на учителя);

определя диапазона от приемливи стойности за ориентацията на референтната равнина на ролковата опора,

В процеса на завършване на курсовата работа е необходимо да се развият следните умения и способности:

определяне на връзки, действащи върху тяло или система от тела;

съставяне на уравнения на равновесие за произволно тяло, включено в системата от тела и намиране на реакциите на връзките;

решаване на проблеми по различни начини.

Фермата на моста е в равновесие под действието на сили и . Геометричните размери на фермата са известни. Фермата лежи в точка върху ролкова опора и в точка е фиксирана от фиксирана панта.

Проучете баланса на фермата. Определете реакциите на външни и вътрешни връзки за различни видове опори и тяхното местоположение (схеми 1, 2, 3).

Изходни данни

1. Определяне на реакциите на външните отношения

За да определите реакциите на външните връзки, помислете за мостова ферма (фиг. 2), съдържаща 8 възела, свързани с 13 пръта. Фермата е в равновесие под действието на активни сили , , , и връзки, приложени в точки и .

Нека освободим фермата от опорите, като заменим тяхното действие със силите на реакциите на свързване. Нека начертаем координатна система и изобразим външните сили, действащи върху нея: активни , , , , и принудителни реакции

Ще насочим реакцията на ролковата опора перпендикулярно на базовата равнина, а реакцията на фиксираната шарнирна опора ще бъде представена от два компонента, т.е. насочването им в положителната посока на координатните оси. Тъй като всички тези сили се намират вравнина, тогава фермата е в равновесие под действието на произволна равнинна система от сили.

Тъй като върху фермата действа произволна равнинна система от сили и условието е изпълнено, фермата е статично определена и фермата може да бъде изчислена с помощта на методите на теоретичната механика.

Нека съставим уравненията на равновесието за системата от сили, действащи върху фермата:

Решавайки последователно системата от уравнения, от второто уравнение намираме реакцията

От третото уравнение на тази система -

и от първото уравнение

Тъй като стойността се оказа отрицателна, реакцията е насочена обратно на посоката, избрана в изчислителната схема.

2. Определяне на силите в пръти за ферми чрез рязане на възли

Методът на рязане на възли се свежда до последователно разглеждане на равновесието на всяка възлова връзка на фермата.

Номерираме възлите на фермата с римски цифри, а прътите с арабски цифри (фиг. 3). Пръчките, събиращи се във възли, са връзки за всяка възлова връзка. Нека изхвърлим връзките и заменим действията им с реакции - сили в прътите, които ще бъдат обозначени със символа . Фигурата показва номерирани възли на ферма с приложени към тях активни и реактивни сили. Тук се взема предвид аксиомата за равенството на силите на действие и противодействие, т.е. Реактивните сили са показани на фигурата при предположението, че прътите са опънати, т.е. насочени встрани от възлите. Тогава реакцията ще бъде положителна, ако прътът е опънат, и отрицателен, ако е компресиран.

Помислете сега за равновесието на възлите на фермата. Силовите системи, действащи върху всеки възел, са силови системи на конвергентна равнина. Равновесието на такива системи от сили е възможно, ако тяхната резултатна е нула. Това условие може да се запише като

Тъй като всеки разглеждан възел трябва да има не повече от дванеизвестни реакции, избираме следната последователност от решения

Нека съставим уравненията на равновесието за всеки от възлите и последователно да намерим реакциите на прътите на фермата.

От уравненията, като се вземат предвид намерените по-рано реакции на външни връзки, намираме реакциите:

От уравненията, като се вземе предвид, (4)

От уравненията , като се вземе предвид

От уравненията, като се вземе предвид (5),

От първото уравнение на системата , като се вземе предвид (7)

Последното уравнение на системата и уравненията могат да служат, с реакциите на външните ограничения, открити по-рано, като такива за проверка. Наистина ли

Обобщаваме резултатите от изчисленията в таблица.

Отрицателните стойности на реакциите на прътите показват, че посоките на тези реакции са противоположни на приетите в проектната схема и следователно те са компресирани. Пръчките при определени стойности на силите на натиск могат да загубят правата си форма (огънат) и при по-нататъшни изчисления те трябва да бъдат проверени, освен за якост, и за стабилност. Стойностите на реакциите на пръчките са положителни. Следователно тези пръти са разтегнати.

Изборът на предложената изчислителна последователност за намиране на желаните реакции се дължи на факта, че решението на уравненията на равновесието е извършено в зависимост от решенията, намерени на предишния етап, т.е. "ръчно". Тази последователност не е уникална. Можете да зададете други последователности от решения.

Когато използвате метода за рязане на възли, можете да направите, без първо да намерите реакциите на външните връзки (реакциите на опорите на фермата). Наистина, статично определена и геометрично непроменлива ферма съдържа пръти, където е броят на възлите; тъй като са необходими три уравнения за намиране на реакциите на опорите, след това за изчисляване на всички неизвестни сили (реакции на опори и реакциипръти) се нуждаят от уравнения.

По отношение на разглежданата ферма имаме 8 възела и 13 неизвестни. Като разгледаме баланса на всички възли на фермата, получаваме затворена система от 14 линейни алгебрични уравнения - , по отношение на 14 неизвестни количества (реакции на външни и вътрешни връзки).

Уравнения , в този случай, може да служи за проверка на изчислението: когато се заменят в тях намерените стойности на реакциите на опорите, те трябва да се превърнат в идентичности.

Този подход е ефективен при използване на компютърна технология, която улеснява решаването на големи системи от линейни алгебрични уравнения.

Следователно, в задачите за намиране на реакциите на външни и вътрешни връзки за ферми, изпълнени съгласно схеми 2 и 3, ние се ограничаваме до съставянето само на уравнения на равновесие и ще ги решим с помощта на пакета Mathcad (раздел 4).

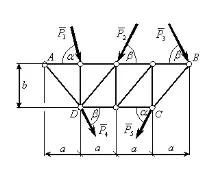
Да разгледаме мостова ферма (фиг. 4 а), която е в равновесие под действието на активни сили , , и връзки, приложени в точки и . В точка А има безтегловен прът, в точка В има шарнирна опора, чийто ъгъл на наклона на опорната равнина е равен на .

Както преди, ще използваме метода за изрязване на възли, за да намерим реакциите на външните и вътрешните връзки. Помислете за равновесието на всеки възел на фермата. Да изхвърлим връзките и да заменим техните действия с реакции: вътрешни – и външни – (фиг. 4 б). Записвайки уравненията на равновесието за всеки възел, получаваме