Диплома - стр. 4
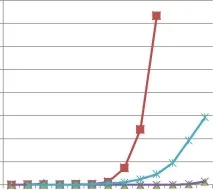
Точно решение
генетичен алгоритъм
Решение, използващо минималното обхващащо дърво
Решение за минимално обхват (оптимизирано k = 3)
Решение за минимално обхват (оптимизирано k = 5
Според изследванията генетичните алгоритми имат средна сложност
O(nt), къдетоnе дължината на хромозомата (т.е. броят на градовете), m -отразява влиянието на размера на популацията и вероятностите на генетичните оператори. Тесното място на генетичните алгоритми е многократното изчисляване на стойността на функцията за годност.
Броят на изчисленията е:
Нека се опитаме да вземем като изходни данни за решаване на задачата на търговския пътник чрез генетичен алгоритъм решенията, получени с помощта на минималното обхващащо дърво със и без оптимизация (Таблица 2.4.4. и Таблица 2.4.5.). При голям брой градове също е необходимо да се промени условието за спиране на алгоритъма.
Таблица 2.4.4 Сравнение на точността на решаване на проблема на пътуващия търговец с помощта на генетични алгоритми с ефективни методи за решаване.
Таблица 2.4.5. – Сравнение на времето за решаване на проблема на пътуващия търговец с помощта на генетични алгоритми с ефективни методи за решаване (време в ms). Набор от данни е решение на проблем, получено с помощта на ефективни методи.
Очевидно е, че решението е с най-добро качество, но броят стъпки за оптимизация, предприети за решаване на проблема с помощта на минималното обхващащо дърво, не го засяга по никакъв начин. От това можем да заключим, че генетичните алгоритми могат да се прилагат след ефективни методи за решение за повишаване на точността. Времето за изпълнение също е значително намалено.
Въз основа на получените резултати можем да направим следния извод: нека има проблем, за който някоиприблизително решение, то за да се подобри полученото решение, то може да се подаде на входа на генетичния алгоритъм. Полученото по този начин решение ще бъде по-точно.
Поради особеностите на тяхната реализация, генетичните алгоритми се поддават добре на паралелизиране, въз основа на това ще проучим тяхната ефективност в този случай.
2.5. Разработване на генетични алгоритми към модел с няколко
2.5.1. Миграционен модел на генетични алгоритми
Генетичните алгоритми се използват и при паралелни изчисления (паралелни реализации).
Първият подход е паралелизиране на отделните стъпки на алгоритъма:
селекция и репликация, мутации, изчисляване на фитнес функция. В този случай популацията е разделена на блокове, всеки от които се обработва от отделна нишка.
Този подход обаче не е много удобен при програмиране.
Най-често използваният е миграционният модел. Миграционният модел представя популацията като набор от подпопулации. Всяка субпопулация се обработва от отделен процесор. Тези субпопулации се развиват независимо една от друга по време на същия брой поколенияT(време на изолация). След изтичане на времето за изолация индивидите се обменят между популациите (миграция, „кражба на булка“). Броят на индивидите, които са били обменени (вероятност за миграция), методът на подбор на индивиди за миграция и моделът на миграция определят честотата на поява на генетично разнообразие в субпопулациите и обмена на информация между субпопулациите.
Изборът на лица за миграция може да се извърши по следния начин:
произволна единна извадка от лица;
пропорционален подбор: най-подходящите индивиди се вземат за миграция.
Разделете субпопулациите паралелногенетичните алгоритми могат условно да се приемат като върхове на някакъв граф. В тази връзка можем да разгледаме топологията на графиката на миграционния генетичен алгоритъм. Най-често срещаната миграционна топология е пълната графика (фиг. 2.5.1.1.), в която индивиди от всяка субпопулация могат да мигрират към всяка друга субпопулация. За всяка субпопулация общият брой на потенциалните „имигранти“ се конструира от всички субпопулации. Мигриращият индивид се избира на случаен принцип от общия брой.
Когато се използва пропорционална селекция при неограничена миграция, първо се формира масив от най-подходящите индивиди, избрани от всички субпопулации. От този масив произволно се избира индивид и с него се заменя най-малко подходящият индивид в субпопулация 1. Подобни действия се извършват и с останалите субпопулации. Но при такава кампания са възможни сблъсъци: че някаква популация ще получи дубликат на своя „добър“ индивид.
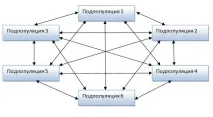
Фигура 2.5.1.1 – Миграция с пълна мрежова топология
Друга основна миграционна схема има пръстеновидна топология (фиг. 2.5.1.2.). Тук индивидите се прехвърлят между съседни (в посока на заобикаляне) популации. Така индивиди от една субпопулация могат да мигрират само към една – съседна популация.
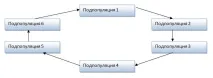
Фигура 2.5.1.2. – Миграция с пръстеновидна топология
Има стратегия за миграция, която съчетава първия и втория модел и също така ви позволява да разрешавате сблъсъци на първия модел. Както при пръстеновидната топология, миграцията възниква само между най-близките съседи, но миграцията в този модел е възможна и между "екстремни" субпопулации (тороидални миграции на ръба). [7]
2.5.2. Островен модел на генетични алгоритми
Островният модел е най-често срещаният моделпаралелен генетичен алгоритъм. Същността му се състои в това, че популацията, като правило, състояща се от много голям брой индивиди, е разделена на субпопулации с еднакъв размер. всяка субпопулация се обработва от избелващия процесор, като се използва една от разновидностите на непаралелния генетичен алгоритъм. Понякога, например на всеки пет поколения, субпопулациите ще обменят няколко индивида.
Такива миграции позволяват на субпопулациите да споделят генетичен материал.
Нека се изпълняват 16 независими генетични алгоритма, като се използват субпопулации от по 100 индивида всяка. Ако няма миграция, възникват 16 независими търсения на решение. Всички търсения се извършват върху различни първоначални популации и се свеждат до определени индивиди. Изследванията потвърждават, че генетичният дрейф има тенденция да води субпопулации до различни доминиращи индивиди. Това се дължи на факта, че, първо, броят на островите, които приемат доминиращи "емигранти" от острова, е ограничен (2-5 острова). Второ, обменът на лица е едностранен. Следователно групи от острови с различни доминиращи индивиди се появяват в голяма популация. Ако популацията е малка, фалшивите доминиращи индивиди могат да мигрират бързо.
Например, истинското решение е само на един остров, а няколко фалшиви доминанти са на други острови. След това, по време на миграцията, броят на фалшивите индивиди на островите ще се увеличи (за всеки остров миграциите се извършват от поне два острова) и правилното решение ще бъде унищожено от генетичния алгоритъм. По този начин, в малка популация с генетичен дрейф, могат да се появят погрешни доминиращи индивиди и алгоритъмът може да се сближи с фалшив оптимум.
Въвеждането на миграцията в островния модел прави възможно намирането на различни доминиращи индивидисубпопулации, което допринася за поддържането на разнообразието в популацията.
Всяка субпопулация може да бъде сбъркана с остров. По време на миграцията субпопулациите обменят своя генетичен материал. При честата миграция на голям брой индивиди генетичният материал се смесва. Това елиминира местните различия между островите. Много редките миграции не предотвратяват преждевременната конвергенция на алгоритъма върху малки популации. IN
В разглеждания модел миграциите от всеки остров могат да се извършват само на определено разстояние: 2-5 скелета, в зависимост от броя на популациите. Така всеки остров е почти изолиран. Броят на островите, към които могат да мигрират индивиди от една субпопулация, се наричаизолационно разстояние.
Трябва да се отбележи, че в такъв модел взаимните миграции са изключени.