добре покрита графика

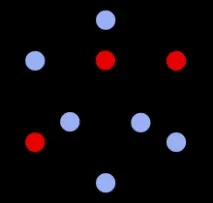
В теорията на графите,добре покрит граф(понякога наричандобре покрит граф) е неориентиран граф, в който всяко минимално покритие на върха има същия размер (като всяко друго минимално покритие на върха). Добре покритите графики са дефинирани и изследвани от Plummer [1] .

Съдържание

Верхово покритие на граф е набор от върхове на граф, така че всяко ребро има поне един край в покритието. Едно покритие е минимално (нередуцируемо), ако премахването на който и да е връх разрушава покритието. Покритието се нарича най-малкото, ако няма друго покритие на графа с по-малък брой върхове. Добре покрита графа е тази, в която всяко минимално покритие е и най-малкото. В своята оригинална статия Плъмър пише [1], че дефиницията на добре покрита графа е „очевидно еквивалентна“ на свойството, че всеки две минимални покрития имат еднакъв размер.

Независим набор от граф е набор от върхове, в който няма два съседни върха. Ако C е покритие на върха на G , допълнението на C трябва да бъде независимо множество и обратно. C е минималното покритие на върха тогава и само ако неговото допълнение I е максималното независимо множество, а C е най-малкото покритие на върха тогава и само ако неговото допълнение е най-голямото независимо множество. По този начин добре покритата графа е, еквивалентно, графика, в която всяко максимално независимо множество е най-голямото.

Комплексът на независимост [en] на графика G е симплициален комплекс, който има симплекс за всяко независимо множество в G . Симплициалният комплекс се нарича прост, ако всички негови максимални симплекси имат една и съща кардиналност, така че добре покритата графае еквивалентен на граф с прост комплекс на независимост [3] .

а	b	° С	д	д	f	ж	ч
8	8
7	7
6	6
5	5
4	4
3	3
2	2
1	1
а	b	° С	д	д	f	ж	ч

Графичен цикъл с дължина четири или пет е добре покрит - и в двата случая максималният независим набор има размер две. Цикъл с дължина седем и път с дължина три също са добре покрити. Всеки пълен граф е добре покрит - всеки максимален независим набор се състои от един връх. Пълният двустранен граф е добре покрит, ако и двете му части имат еднакъв брой върхове - той има само две максимални независими множества. Графиката на топа е добре покрита - ако поставите произволен набор от топове на шахматната дъска, така че два топа да не се атакуват един друг, винаги можете да добавите друг неатакуващ топ, докато има топ на всеки ред и колона.

Ако P е многоъгълник или набор от точки, S е набор от отворени интервали, имащи върхове на P като крайни точки и без точки на P вътре, и G е пресечна графика на S (графа, имаща върхове за всеки интервал в S и ребро за всяка двойка пресичащи се интервали), тогава G е добре покрит. За този случай всеки максимален независим набор в G съответства на набор от ръбове в многоъгълна триангулация P и изчисляването на характеристиката на Ойлер показва, че всеки две триангулации имат еднаквисъщия брой ръбове [4] .

Ако G е която и да е графа с n върха, коренният продукт [en] на G с граф с едно ребро (т.е. графиката H, образувана чрез добавяне на n нови върха към G, всеки със степен едно и всички свързани с различни върхове, в G) е добре покрит. Максималното независимо множество в H трябва да се състои от произволно независимо множество в G, заедно със съседи от степен едно, от допълнително множество. Така това множество има размер n [5] . По-общо казано, като се има предвид всеки граф G заедно с покритие на клика (разделяне на p върхове на G на клики), графът G p, образуван чрез добавяне на връх за всяка клика, е добре покрит. Коренният продукт е частен случай на тази конструкция, когато p се състои от n клики, съдържащи по един връх [6] . Така всеки граф е генериран подграф на добре покрит граф.

Фаварон дефинирамного добре покрит графкато добре покрит граф (евентуално несвързан, но без изолирани върхове), в който всяко максимално независимо множество (и следователно също всяко минимално покритие на върхове) съдържа точно половината от върховете [2] . Тази дефиниция включва коренните произведения на графа G и графа с едно ребро. Това също включва, например, двустранни добре покрити графи, изследвани от Ravindra и Berge [7] [8] — в двустранен граф без изолирани върхове, двете страни на всяка част образуват максимални независими набори (и минимални покрития на върхове), така че ако графът е добре покрит, и двете страни трябва да имат еднакъв брой върхове. В добре покрит граф с n върха, размерът на максималното независимо множество не надвишаваn/2, така че много добре покритите графи са добрипокрити графове, в които най-голямото независимо множество има максималния възможен размер за графове [8] .

Двуделният граф G е добре покрит тогава и само ако е перфектно съвпадение на M със свойството, че за всяко ребро uv от M генерираният подграф от съседи u и v образува пълен двуделен граф [7] [9] . Характеризирането по отношение на съвпаденията може да бъде разширено от двустранни графи до много добре покрити графи - граф G е много добре покрит тогава и само ако графиката има перфектно съвпадение M със следните две свойства:

1. Нито един ръб на M не принадлежи на триъгълник в G ;
2. Ако M е централното ребро в път, състоящ се от три ребра в G, тогава двата крайни върха на пътя трябва да са съседни.

Въпреки това, ако G е много добре покрито, тогава всяко перфектно съвпадение в G удовлетворява тези свойства [10] .

Дърветата са специален случай на двустранни графи и тестването дали дървото е добре покрито може да се разглежда като много прост случай на характеризиране на добре покрити двустранни графи — ако G е дърво с повече от два върха, то е добре покрито тогава и само ако всеки нелистов ръб на дървото е съседен на точно един лист [7] [9] . Същата характеристика се прилага за графи, които са локално като дървета, в смисъл, че близкото съседство на всеки връх е ациклично – ако графът има обиколка от осем или повече (така че за всеки връх v, подграф от върхове на разстояние три от v е ацикличен), тогава той е добре покрит тогава и само ако всеки връх със степен по-голяма от две има точно един съсед със степен едно [11] . Тясно свързана, но по-сложна характеристика се прилага задобре покрити графики с обиколка пет или повече [12] [13] .

---