Движения в гредите по време на огъване

Видове движения при навеждане

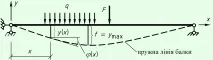
Еластичната линия на гредата е оста на гредата след деформация.

Отклонението на лъча $y$ е постъпателното движение на центъра на тежестта в напречната посока на лъча. Считаме отклонението нагоре за положително, отклонението надолу за обемно.

Уравнението на еластичната линия е математическо представяне на зависимостта $y(x)$ (огъване по дължината на гредата).

Деформационна стрела $f = >$ - максималната стойност на деформация на гредата по дължината.

Ъгъл на завъртане на сечението $\varphi $ – ъгъл, под който сечението се завърта по време на деформация на гредата. Ъгълът на завъртане се счита за положителен, ако секцията се върти обратно на часовниковата стрелка и обратно.

Ъгълът на завъртане на сечението е равен на ъгъла на наклона на еластичната линия. По този начин функцията за промяна на ъгъла на въртене по дължината на гредата е равна на първата производна на функцията на отклонение $\varphi (x) = y'(x)$.

Така при огъване разглеждаме два вида премествания - отклонение и ъгъл на завъртане на сечението.

Цел на дефиницията на преместването

Движенията в прътовите системи (особено в гредите) се определят, за да се осигурят условия за твърдост (деформациите са ограничени от строителните норми).

В допълнение, дефинирането на преместванията е необходимо за изчисляване на якостта на статично неизпъкнали системи.

Диференциално уравнение на еластична линия (крива ос) на греда

На този етап е необходимо да се установи зависимостта на преместванията в гредата от външни натоварвания, метода на закрепване, размерите на гредата и материала. За пълно решение на задачата е необходимо да се получи функцията на отклонение $y(x)$ по цялата дължина на гредата. Съвсем очевидно е, че преместванията в гредата зависят от деформациите на всяко сечение. Преди това получихме зависимостта на кривината на сечението на гредата от огъващия момент, действащ в този участък.

Определя се кривината на линиятанеговото уравнение $y(x)$ така

където $y'$ и $y$ са съответно първата и втората производни на функцията на отклонение с координатаx.

От практическа гледна точка тази нотация може да бъде опростена. Всъщност $y' = \varphi $ - ъгълът на въртене на сечението в реални конструкции не може да бъде голям, като правило, не повече от 1deg = 0,017rad. Тогава $1 + \right)^2> = 1 + = 1,000289 \приблизително 1$, тоест можем да приемем, че $\frac = y" = \fracy>>>>$. Така получихме уравнението на еластичната линия на гредата (диференциалното уравнение на огънатата ос на гредата). Това уравнение е получено за първи път от Ойлер.

$y(x)$ – функция на отклонение;

$y'(x) = \varphi (x)$ – функция на ъгъла на завъртане;

$EI \cdot y"(x) = M(x)$ – функция за промяна на огъващия момент;

$EI \cdot y"'(x) = M'(x) = Q(x)$ – функция за промяна на силата на срязване;

$EI \cdot >(x) = M"(x) = q(x)$ е функцията за промяна на напречното натоварване.

---