Джобно сортиране
Pocket sort(англ.Bucket sort) е алгоритъм за сортиране, базиран на предположението за равномерно разпределение на входните данни.
Как работи[редактиране]
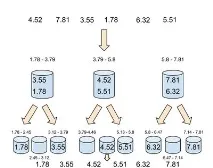
За сортиране на джобове трябва да разделите елементите на масива с входни данни на [math]k[/math] блокове (джобове, кошници). След това всеки от тези блокове се сортира или по друг сорт, или рекурсивно по същия метод на разделяне. След сортиране във всеки блок, данните се записват в масива в реда, в който са били разделени на блокове. В същото време трябва да се има предвид, че това сортиране работи само ако разделянето на блокове е направено по такъв начин, че елементите на всеки следващ блок да са по-големи от предишния.
Pocketsort се влошава много с голям брой леко различни елементи (повечето от елементите ще попаднат в една кошница). Следователно този тип сортиране трябва да се използва, когато има голяма вероятност числата да се повтарят рядко (например поредица от произволни числа).
Внедряване[редактиране]
Има няколко различни реализации на джобно сортиране.
Помислете за рекурсивни и нерекурсивни реализации.
Рекурсивно сортиране в кофа[редактиране]
Помислете за кода за рекурсивна реализация на джобно сортиране.
Входът е реални числа.
Нерекурсивна реализация[редактиране]
Нека [math]n[/math] е броят на елементите в масива, [math]k[/math] е броят на блоковете за разделяне.
[math] n_i [/math] е произволна стойност, указваща броя на елементите в [math] i [/math] -тия джоб.
[math] T(n) = \Theta(n) + \sum\limits_^k O(n_i[/math] [math] \log n_i) + \Theta(k)[/math] , където [math] T(n) [/math] е времето на изпълнение на алгоритъма за джобно сортиране.
[math] E[n_i] = \dfrac [/math]
Тоест, ако [math] n \sim k \Rightarrow E[T(n)] = \Theta(n) [/math]
Ако [math] n = o(k) \Rightarrow E[T(n)] = \Theta(k)[/math]
От горните формули може да се види, че средно "джобното сортиране" се изпълнява в линейно време.