Формули и уравнения, които промениха света, астрономията и астронавтиката днес

Математикът Иън Стюарт, в новата си книга В търсене на неизвестното: 17 уравнения, които промениха света, разглежда някои от най-важните уравнения на всички времена и дава примери за техните практически приложения.

Питагорова теорема

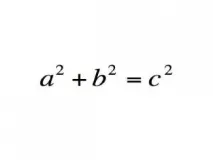
Според Питагоровата теорема в правоъгълен триъгълник квадратът на дължината на хипотенузата е равен на сумата от квадратите на дължините на катетите.

Важност : Питагоровата теорема е най-важното уравнение в геометрията, което я свързва с алгебрата и е в основата на тригонометрията. Без него би било невъзможно да се създаде точна картография и навигация.

Съвременни употреби : Триангулацията все още се използва днес за точно определяне на относителната позиция за GPS навигация.

Логаритъм и неговата идентичност

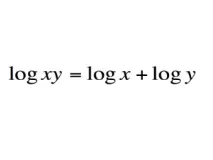
Логаритъм и неговата идентичност

Логаритъмът е степента, на която трябва да се повдигне основата, за да се получи аргументът.

Важност : Логаритмите се превърнаха в истинска революция, позволявайки на астрономите и инженерите да правят изчисления по-бързо и по-точно. С появата на компютрите те не са загубили своето значение, тъй като все още са от съществено значение за учените.

Съвременна употреба : Логаритмите са важна част от разбирането на радиоактивния разпад.

Основна теорема на анализа

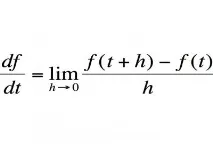
Основна теорема на анализа

Основната теорема на анализа илиформулата на Нютон-Лайбниц дава връзката между две операции: вземане на определен интеграл и изчисляване на първоизводната.

Важност : Теоремата за анализа всъщност създаде съвременния свят. Смятането е от съществено значение за нашето разбиране за това как да измерваме твърди тела, криви и площи. Тя е в основата на много природни закони и източникдиференциални уравнения.

Модерна употреба : Всеки математически проблем, при който се изисква оптимално решение. От съществено значение за медицината, икономиката и информатиката.

Класическата теория на гравитацията на Нютон

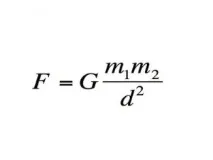
Класическата теория на гравитацията на Нютон описва гравитационното взаимодействие.

Важност : Теорията ви позволява да изчислите силата на гравитацията между два обекта. Въпреки че по-късно беше заменена от теорията на относителността на Айнщайн, теорията все още е необходима за практическо описание на това как обектите взаимодействат един с друг. Ние го използваме и до днес, за да проектираме орбитите на сателити и космически кораби.

Модерна употреба : Позволява ви да намерите най-енергийно ефективните начини за изстрелване на сателити и космически сонди. Също така прави възможна сателитна телевизия.

Комплексни числа

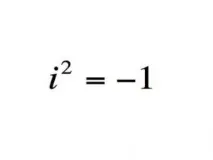
Комплексните числа са разширение на полето от реални числа.

Важност : Много съвременни технологии, включително цифрови фотоапарати, не биха могли да бъдат изобретени без комплексни числа. Те също така позволяват анализа, от който инженерите се нуждаят за решаване на практически проблеми в авиацията.

Модерна употреба : Широко използван в електротехниката и сложните математически теории.

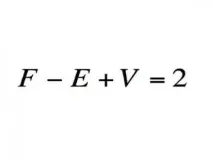
Ойлерова характеристика на многостените

Важност : Допринесе за разбирането на топологичното пространство, в което се разглеждат само свойствата на непрекъснатостта. Основен инструмент за инженери и биолози.

Модерна употреба : Топологията се използва за разбиране на поведението и функцията на ДНК.

Нормална дистрибуция

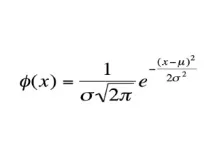
Модерна употреба : Използва се в клинични изпитвания за определяне на ефективността на лекарствата спрямо отрицателните странични ефекти.

вълново уравнение

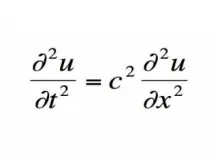
Диференциално уравнение, описващо поведението на вълните.

Важност : Вълните се изучават, за да се определи времето и мястото на земетресенията, както и да се предвиди поведението на океана.

Модерна употреба : Петролните компании използват експлозиви и след това четат данни от последващи звукови вълни, за да определят геоложки формации.

Преобразуване на Фурие

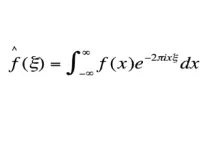
Важност : Уравнението ви позволява да прекъсвате, почиствате и анализирате сложни модели.

Модерна употреба : Използва се за компресиране на информация за JPEG изображения и за откриване на структурата на молекулите.

Уравнения на Навие-Стокс

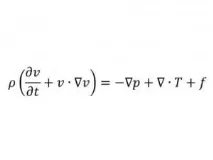
От лявата страна на уравнението е ускорението на малко количество течност, от дясната страна са силите, които действат върху него.

Важност : След като компютрите станаха достатъчно мощни, за да решат това уравнение, те отвориха сложна и много полезна област на физиката. Той е особено полезен за създаване на по-добра аеродинамика в превозните средства.

Съвременни употреби : Освен всичко друго, уравнението е помогнало за подобряването на съвременните пътнически самолети.

Уравнения на Максуел

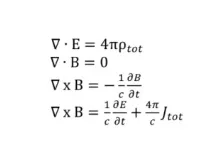
Опишете електромагнитното поле и връзката му с електрическите заряди и токове във вакуум и непрекъсната среда.

Важност : Помогна за разбирането на електромагнитните вълни, което допринесе за много от технологиите, които използваме днес.

Съвременни употреби : радар, телевизия исъвременни средства за комуникация.

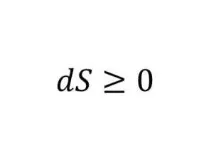
Втори закон на термодинамиката

Цялата енергия и топлина в крайна сметка ще изчезнат.

Важност : От съществено значение за нашето разбиране за енергията и вселената чрез концепцията за ентропия. Откриването на закона помогна за подобряването на парната машина.

Съвременни употреби : Помогна да се докаже, че материята е изградена от атоми, знание, което физиците използват и до днес.

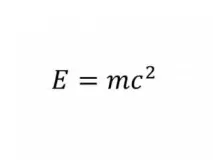
Теорията на относителността на Айнщайн

Енергията е равна на масата по скоростта на светлината на квадрат.

Важност : Вероятно най-известното уравнение в историята. Това напълно промени гледната ни точка за материята и реалността.

Съвременни употреби : Помогнал за създаването на ядрени оръжия. Използва се в GPS навигацията.

Уравнение на Шрьодингер

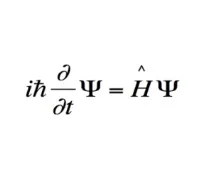
Нелинейно уравнение на Шрьодингер

Описва материята като вълна, а не като частица.

Важност : Обърна гледната точка на физиците - частиците могат да съществуват в набор от възможни състояния.

Модерна употреба : Значителен принос към използването на полупроводници и транзистори и по този начин към по-голямата част от съвременните компютърни технологии.

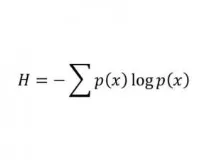
Информационна ентропия на Шанън

Оценява количеството данни в част от кода чрез изчисляване на вероятността на неговите знаци.

Важност : Това е уравнението, което отвори вратата към информационната ера.

Модерна употреба : Почти всичко, свързано с откриването на грешки в кодирането (програмирането).

Логистичен модел на нарастване на населението

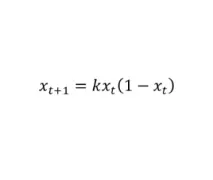
Логистичен модел на растежпопулации

Оценка на промените в популацията на живи същества от поколение на поколение с ограничени ресурси.

Важност : Помогна за развитието на теорията на хаоса, която напълно промени нашето разбиране за това как работят природните системи.

Модерна употреба : Използва се за симулация на земетресение и прогнозиране на времето.

Модел Блек-Шоулс

Моделът на Блек Скоулс

Един от вариантите на ценовите модели.

Значение : Помогна за създаването на няколко трилиона долара. Според някои експерти злоупотребата с формулата (и нейните производни) е допринесла за финансовата криза. По-специално, уравнението има няколко допускания, които не са верни на реалните финансови пазари.

Съвременна употреба : Дори след кризата се използва за определяне на цените.

Вместо заключение

В света има много други важни уравнения и формули, които са променили съдбата на човечеството като цяло и личния ни живот в частност. Сред тях моделът на Ходжкин-Хъксли, филтърът на Калман и, разбира се, уравнението на търсачката Google. Надяваме се, че сме успели да покажем колко важна е математиката и колко безценен е нейният принос за всички хора.