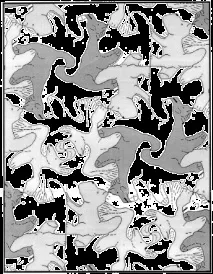
Геометрични трансформации и паркети
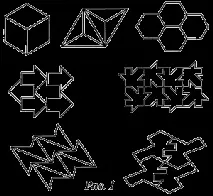
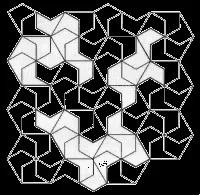
Сред огромното разнообразие от орнаменти се открояват "паркети" (мозайки). Паркетът е запълване на равнина с еднакви фигури (паркетни елементи), които не се припокриват една с друга и не оставят празно пространство в равнината (понякога паркетът се нарича запълване на равнина с няколко фигури, например правилни многоъгълници). Кариран лист тефтер е най-простият паркет. Паркетният елемент тук е квадрат. Елементът на паркета е също равностранен триъгълник, правилен шестоъгълник, произволен успоредник, дори произволен четириъгълник. Можете да измислите стотици, хиляди различни паркетни елементи. Някои от тях са показани на фиг. 1.
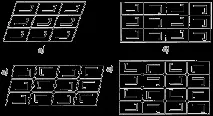
Изобретени са паркетите, при които няколко елемента образуват фигура, подобна на паркетен елемент. Примери за такива паркети са показани на фиг. 2.
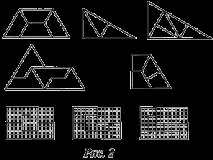
На фиг. Фигура 3 показва елемент от обикновен паркет, който е разделен на фигурата вдясно на четири еднакви фигури - елементи от нов паркет. И на фиг. 4 са показани елементите на новия паркет, състоящ се също от четири такива фигури.

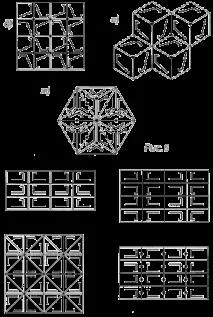
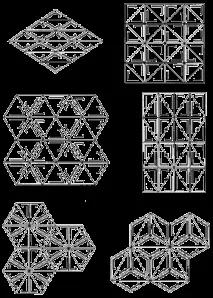
Общо има 17 вида симетрия на мрежестите орнаменти. Те са показани схематично на фиг. 6 и 7. Първите седем от тях (фиг. 6, a-g) позволяват създаването на интересни паркети без праволинейни контури.
Паркетите са отличен материал за въвличане на учениците в интересни, смислени и поучителни дейности при изучаването на някои теми от училищния курс по математика. В този случай забавлението няма външен, формален характер, а насърчава учениците да изяснят същността на изучавания материал. Успешно могат да се използват в 5-9 клас в класната стая и след учебните часове.Прекрасните паркети са проектирани от известния холандски художник Морис Ешер. Неговите паркетни елементи бяха фигури на животни, птици, влечуги.
Най-простият тип паркет е този, при който равнината е изпълнена с фигури с помощта на паралелен превод.
Общата му схема е показана на фигура 6, а. Полезно е да се използват такива паркети при изучаването на паралелния транспорт, включвайки и описание с помощта на формули, т.е. алгебричен метод.
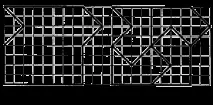
Задача 1. На фиг. Фигура 8 показва (все още не е наличен. E.S.) паркет, тоест запълването на цялата равнина с еднакви (равни) фигури. Както се вижда от фигурата, този паркет може да се комбинира със себе си чрез различни успоредни прехвърляния, например три клетки надясно и една клетка нагоре. Това паралелно прехвърляне се дава от двойка числа (3; 1). Този паркет също се комбинира със себе си чрез паралелен трансфер, който се характеризира с двойка числа (- 6; - 2) или двойка (- 2; 3). Виж това!
- Напишете още 8-10 двойки числа, които определят паралелни преводи, които комбинират този паркет със себе си.
- Направете това за паркети, които могат да се получат чрез успоредно пренасяне на всяка от фигурите, представени на фиг. 9.

- Анализирайте получените двойки числа за всеки паркет. Въведете за тях операциите събиране, изваждане и умножение с цяло число. Посочете две двойки числа, така че останалите да се получат от тях чрез въведените операции.
Задача 2. Премествайки фигурата чрез паралелен трансфер (фиг. 10, a, b), запълнете цялата равнина с нея. Характеризирайте всеки паркет с двойки числа - координатите на векторите, които определят паралелните транслации на предложената фигура. Намерете сумата, разликата на всеки два получени вектора или произведението на тези вектори с цяло число.Какъв вектор ще получите във всеки случай? Дали паралелната транслация, дадена от този вектор, ще подравни паркета със себе си?
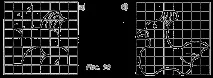
Тези две задачи са подобни една на друга, въпреки че са формулирани на различни езици. Правейки ги, учениците откриват тясна връзка между паралелните трансфери и векторите. В тези задачи ясно се проследява възможността за разлагане на всеки вектор от полученото векторно пространство по отношение на два базисни вектора. Заданията предоставят по-осезаеми и по-лесни за разбиране примери за операции с вектор, вектор и числа.
- Каква фигура получихте?
- Преместете дадените и получените фигури със 7 единични сегмента надясно или наляво. Какво получи?
- Напълнете самолета с тази фигура, като получите паркета.
- Напълнете самолета с предложената фигура, като получите паркета.
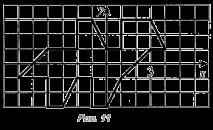
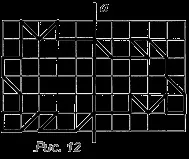
Цифрите на фиг. 11 и 12 са паркетни елементи, чиято обща схема е показана на фиг. 6б.
Задача 5. На фиг. 13 показва запълването на равнината с фигура, даваща паркет, чиято обща схема е показана на фиг. 6, в. Определете центровете на симетрия на този паркет. Продължете да запълвате равнината с тази фигура.
Задача 6.
- Построете фигура, симетрична на дадената спрямо всяка от двете отбелязани точки (фиг. 14). Запълнете самолета с тази фигура.

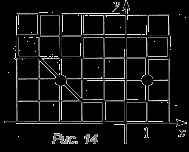
Упражнение7.
- За всяка възлова точка на фигурата, показана на фиг. 14, намерете нейните координати ( x ; y ) и построете в същата система точки с координати ( X ; Y ), намиращи се по формулите: X = - x - 6, Y = - y + 4. Свържете получените точки в същия ред. Какво получи?
Задача 8.
- Посочете трансформациите (една или две), които една от фигурите, показани на фиг. 15 се прехвърлят на друг.
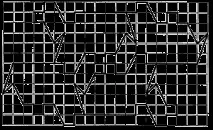
- Въведете координатна система и опишете в координати една от трансформациите, която съчетава дадения паркет със себе си.
- Продължете да запълвате равнината с предложената фигура.
Задача 9.
- На всяка от фиг. 16-18 показват центровете на ротации, които прехвърлят една фигура в друга.
- Запълнете равнината с предложените фигури, като получите паркет тип E, F и G (фиг. 6).
- Намерете центровете на симетрия на получените паркети, ако има такива.

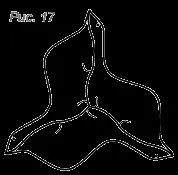
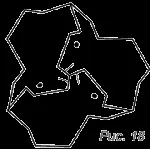
Задача 10. Всяка от фигурите на фиг. 19 запълване на самолета, получаване на паркета. За да направите това, копирайте фигурите върху паус.
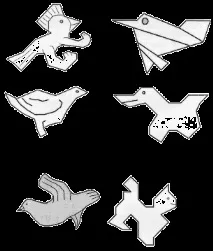
Задача 11. Сравнете фигурите на фиг. 20. Копирайте ги върху проследяващата хартия и запълнете равнината, като получите паркета.








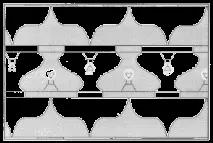


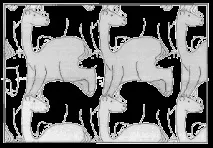





Тези паркети могат да се използват по различни начини. В 5-6 клас е полезно да се предложи на учениците фигура - елемент от паркет, уголемен иизрязани от картон, така че да запълнят самолета с него. Това допринася за формирането на геометрична визия при учениците.
При изучаване на координати и вектори се използват задачи, подобни на дадените по-горе. И, разбира се, те са естествено приложими при изучаването на геометричните трансформации.
Паркетите могат да се използват и при изучаване на темата „Площи на равнинни фигури“ за онагледяване на идеята, че на единица площ може да се избере произволна (квадратна) фигура, например елемент от паркет, както и за намиране на многоъгълника, посочен в задача 12.
За паркета, показан на фиг. 21, площта на фигурката (пеликан) е равна на площта на успоредник с върхове в точки, които са очите на четири съседни птици. За други фигури такива многоъгълници се намират без особени затруднения.
В заключение представяме паркета (фиг. 37), в който са използвани три различни фигури. Получава се от паркета, показан на фиг. 33, като замените фигурите на кучетата с нови фигури. Площите на всички паркетни фигури са равни.