ХАРМОНИЧНИ ТРЕПТЕНИЯ И ТЕХНИТЕ ПАРАМЕРИ - Студиопедия

Дефиниране на проблем

ПО ВРЕМЕ НА ХАРМОНИЧНО ВЪЗДЕЙСТВИЕ

СЕКЦИЯ 2 ЛИНИЙНИ ВЕРИГИ

По вид елементи.

a)Резистивната верига се състои само от резистори R;

b)Реактивна верига се състои само от L и C;

Схеми, съдържащи пасивни елементи, се наричат ​​пасивни вериги. Схеми, съдържащи активни елементи (транзистори, лампи, операционни усилватели) се наричат ​​активни вериги. Пасивните вериги не усилват сигнала, но активните го правят.

Всеки сигнал със сложна форма може да се разложи на редица прости сигнали, напримерхармонични. Тази серия се наричаспектър на сигнала. За линейни веригипринципът на суперпозиция (суперпозиция) е приложим. Същността му е, чеако въздействието е представено от сумата от въздействията, тогава реакцията ще се състои също от сумата от отговорите, получени от всяко въздействие поотделно.

Този принцип е в основата на много методи за анализ (изчисление) на линейни вериги, по-специално в спектралния метод (метод на Фурие). В тази връзка трябва да се научите как да изчислявате веригата под въздействието на един хармоник - хармоничен сигнал.

От теорията на линейните диференциални уравнения е известно, че ако действието е хармоничноx(t) = Хm∙cos(ωt +φ0) с честота w, тогава отговорът ще бъде хармониченy(t) = Ym∙cos(ωt +φy) със същата честота w.

Следователно решението на задачата за изчисляване на реакциятаy(t)се свежда до определяне само на два от трите параметъра -Ymи φ.

Нека въздействиетоx(t) = Хm∙cos(ωt+φ0), напримерu(t) = Um∙cos(ωt +φ0). Тук

Xm–амплитуда (максимална стойност) на флуктуациите;

X = Xm/√2‾ -ефективна стойност ;

ω–ъглова честота [rad/s];

f =1/T-циклична честота [Hz];

T –период на трептене [s];

θ(t) =(ωt +φ0) – косинусният аргумент се наричапълна фаза (самофаза ) на хармоничното трептене;

φ0 = θ(0)–начална фаза. Определя стойността на хармоничната функция приt= 0 –x(0) =Хm∙cos(φ0), т.е. определя позицията на хармоничната функция върху времевата ос, променя се в интервала [–π, π].

Нека θ(t0) =(ωt0+φ0) = 0. Тогаваu (t0) = Um∙cos(ωt0+φ0) =Um- хармоничното трептене има максимална стойност. Следователно точкатаt0 на времевата ос се определя от началната фаза при дадена честота ω

Сравнение на две хармонични трептения с еднаква честота ω.

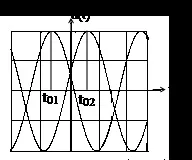
t

t02

t01

Две хармонични трептения могат да се сравняват едно с друго не само по амплитуда, но и в началната фаза, т.е. по позиция върху времевата ос (виж фиг.). Може да се приеме, че точкитеt = t01иt = t02са началото на функциите, т.е. произхода на двата сигнала. След това, чрез стойността на разликатаt12 = t01 - t02, можете да определите кой от сигналите е пред другия сигнал. Акоt12> 0, тогава казваме, че трептенетоu1 (t) е напред във фазана трептенетоu2 (t). Акоt12 0, тогава трептенетоu1 (t) е напред във фазана трептенетоu2 (t). Ако ψ12

Не намерихте това, което търсихте? Използвайте търсачката:

Деактивирайте adBlock! иопреснете страницата (F5)много е необходимо

---