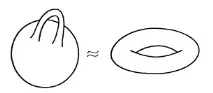
Хомеоморфни разновидности
Преобразуване от едно многообразие в друго се наричахомеоморфизъм, ако установява съответствие едно към едно между тях, непрекъснато и в двете посоки. Разглежданите многообразия се наричат хомеоморфни. Хомеоморфните многообразия имат едно и също измерение и могат да бъдат затворени само едновременно.
Класификацията на многообразията по отношение на хомеоморфизмите е една от основните задачи натопологията -
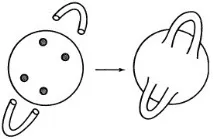
Най-простото такова многообразие есфера. Останалите се получават от сферата чрез следната конструкция. Нека си представим, че сферата е направена от някакъв пластичен материал, например пластилин. Нека направим 2g дупки в него, разделяме тези дупки на двойки и залепваме към краищата на дупките на всяка двойка ръбовете на тръба, изработена от същия материал (необходими са общо g тръби). Чрез изглаждане на линиите на свързване получаваме затворено двумерно многообразие, наречено сфера с g дръжки (фиг. вдясно).
Една обикновена сфера може да се разглежда като сфера с дръжки g=0. Сфера с една дръжка е хомеоморфна наторус — добре познатата повърхност на багела(фиг. вляво). Две сфери с дръжки са хомеоморфни, ако имат еднакъв брой дръжки. Така се оказва, че всяко затворено двумерно подмногообразие в $R^3$ е хомеоморфно на обединението на краен брой по двойки несвързани сфери с дръжки (всяка сфера има свой собствен брой дръжки).
Нека разгледаме по-подробно сферата с дръжки. Очевидно есвързан колектор. Това означава, че човек може да стигне от всяка точка на многообразието до всяка друга точка от него, като се движи по колектора по някаква непрекъсната крива (тоест по образа на сегмент, когато той е непрекъснато картографиран в многообразие). Казва се, че свързано подмногообразие в $R^n$ е просто свързано, ако всяка верига на подмногообразието (т.е. непрекъсната крива, чиито крайни точки съвпадат) може да бъде влачена по колектора чрез непрекъсната деформация вътре в топка с произволно малък радиус, центрирана във всяка точка на това многообразие.