Интегрална теорема на Моавр-Лаплас и условия за нейната приложимост

Интегрална теорема на Моавр-Лаплас. Ако вероятността p за възникване на събитие A във всеки опит е постоянна и различна от 0 и 1, тогава вероятността броят m на възникване на събитие A в n независими опита да лежи в границите от a до b (включително), с достатъчно голямо число n, е приблизително равна на

,

Където

е функцията (или интеграл от вероятности) на Лаплас;

,.

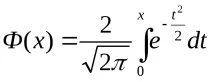
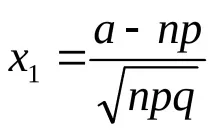
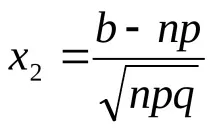
Формулата се нарича интегрална формула на Моавр-Лаплас. Колкото по-голямо е n, толкова по-точна е тази формула. Когато е изпълнено условието npq ≥ 20, интегралната формула

, както и локалната, по правило дава задоволителна за практиката грешка при изчисляване на вероятностите.

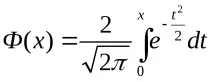
Функцията Ф(х) е таблична (виж таблицата). За да използвате тази таблица, трябва да знаетесвойствата на функцията:

Функцията Ф(х) е нечетна, т.е. F(-x) = -F(x).

Функцията Ф(х) е монотонно нарастваща и при x → +∞ Ф(х) → 1 (на практика можем да приемем, че вече за x > 4 Ф(х) ≈ 1).

Пример. В някои райони на всеки 100 семейства 80 имат хладилници. Изчислете вероятността от 300 до 360 (включително) семейства от 400 да имат хладилници.

Решение. Прилагаме интегралната теорема на Moivre-Laplace (npq = 64 ≥ 20). Нека първо дефинираме:

,

.

Сега, съгласно формулата, като вземем предвид свойствата на Ф(х), получаваме

.

(според таблицата F(2.50) = 0.9876, F(5.0) ≈ 1)

Следствия от интегралната теорема на Моавр-Лаплас (с извеждане). Примери.

Нека разгледаме следствието от интегралната теорема на Моавър-Лаплас.

Последствие. Ако вероятността p за настъпване на събитие А във всеки опит е постоянна и различна от 0и 1, тогава за достатъчно голям брой n независими опити, вероятността, че:

а) броят m на появяванията на събитие А се различава от произведението np с не повече от ε > 0 (по абсолютна стойност), т.е.

;

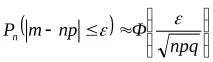
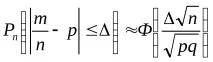
б) честотата

на събитие А е в диапазона от α до β (включително), т.е. , където,.

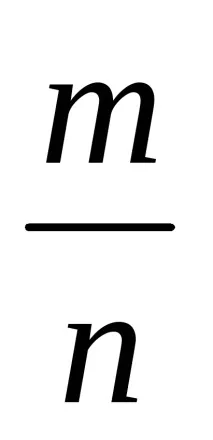
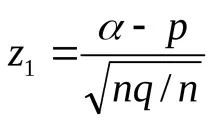
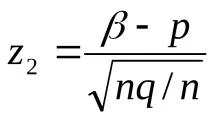
c) честотата

на събитие А се различава от неговата вероятност p с не повече от Δ > 0 (по абсолютна стойност), т.е..

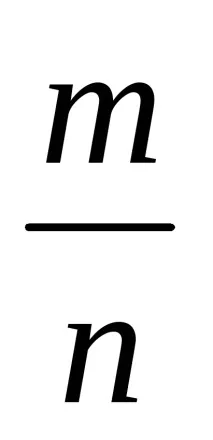
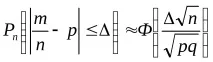
□ 1) Неравенството

е еквивалентно на двойното неравенство pr - E

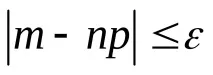
pr + E. Следователно, според интегралната формула:

.

2) Неравенството

е еквивалентно на неравенството a ≤ m ≤ b за a = nα и b = nβ. Заменяйки стойностите a и b във формулите и,с получените изрази, получаваме формулите за доказване и,.

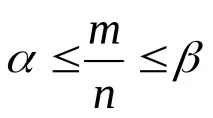
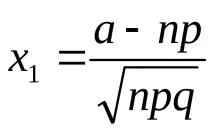
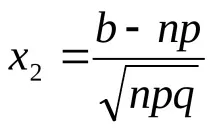
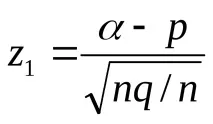
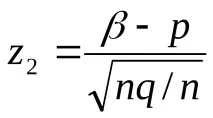
3) Неравенството

е еквивалентно на неравенството. Заменяйкивъв формулата, получаваме формулатаза доказване.

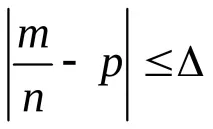
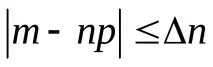
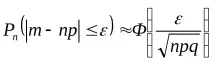
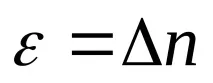
Пример. Според статистиката средно 87% от новородените живеят до 50 години. Намерете вероятността от 1000 новородени делът (честотата) на доживелите до 50-годишна възраст: а) да бъде в границите от 0,9 до 0,95; б) ще се различава от вероятността за това събитие с не повече от 0,04 (по абсолютна стойност)?

Решение. а) Вероятността p едно новородено да доживее до 50 години е 0,87. защото n = 1000 е голямо (условието npq = 1000 0,87 0,13 = 113,1 ≥ 20 е изпълнено), тогава използваме следствието от интегралната теорема на Moivre-Laplace. Нека първо дефинираме:

, . Сега по формулата:

.

Б) Съгласно формулата

:

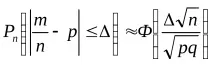
. Тъй като неравенство

е еквивалентно на неравенство, полученият резултат означава, че практически е сигурно, че от 0,83 до 0,91 от броя новородени на 1000 ще доживеят до 50 години.

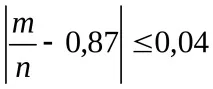
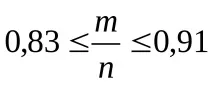
Концепцията за "случайна променлива" и нейното описание.Дискретнаслучайна величина и нейният закон на разпределение (серии). Независимислучайни променливи. Примери.

Случайна променливасе разбира като променлива, която в резултат на тестове, в зависимост от случая, приема една от възможните групи от своите стойности (коя не е известна предварително).

Примери за случайни променливи: 1) броят на децата, родени през деня в Москва; 2) броят на дефектните продукти в дадена партида; 3) броят на изстрелите преди първото попадение; 4) обхват на полета на артилерийски снаряд; 5) консумация на електроенергия за pr-ция на месец.

Случайна променлива се наричадискретна (прекъсната), ако наборът от нейните стойности е краен или безкраен, но изброим.

Поднепрекъсната случайна променливаще разбираме стойността, безкраен неизброим набор от стойности, от които е някакъв интервал (краен или безкраен) на числовата ос.

И така, в горните примери 1-3 имаме дискретни случайни променливи (в примери 1 и 2 - с краен набор от стойности; в пример 3 - с безкраен, но изброим набор от стойности); а в примери 4 и 5 - непрекъснати случайни величини.

Определение. Случайна променлива X е функция, дефинирана върху набор от елементарни резултати (или в пространството на елементарни събития), т.е.

, където където ω е елементарен резултат (или елементарно събитие, принадлежащо на пространството Ω, т.е..

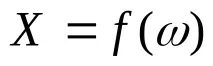
Задискретна случайна променливамножеството

от възможните стойности на случайната променлива, т.е. функции, крайно или изброимо, занепрекъснати- безкрайно и безбройно.

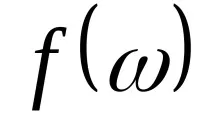
Случайните променливи се означават с главни букви на латинската азбука X, Y, Z. и техните стойности са съответнималки букви x,y,z.

Определение. Законът за разпределение на случайна променлива е всяко отношение, което установява връзка между възможните стойности на случайна променлива и съответните им вероятности.

Казва се, че една случайна променлива е "разпределена" според даден закон за разпределение или "подчинена" на този закон за разпределение.

За дискретна случайна променливазаконът за разпределение може да бъде дадени под формата на таблица, аналитично (под формата на формула) и графично.

Най-простата форма за определяне на закона за разпределение на дискретна случайна променлива X е таблица (матрица), която изброява във възходящ ред всички възможни стойности на случайната променлива и съответните им вероятности, т.е.

---