Изграждане на метла
Развитието е фигура, получена чрез комбиниране на повърхност с равнина. Естествено, затворена повърхност не може да се комбинира с равнина без прекъсвания. Първо, повърхността се нарязва по няколко линии и след това се комбинира с равнината. Изграждането на повърхностни разработки е от голям практически интерес при проектирането на различни конструкции и изделия от листов материал. При разработката се записват дължините на линиите, лежащи върху повърхността, ъглите между линиите и площите на фигурите, образувани от затворени линии. За да се изгради повърхностна разработка, е необходимо да се знае законът за трансформация на повърхностните направляващи линии в линии на развойната равнина и законът за разпределение на правите линии, съответстващи на повърхностните генератори. Законът за превръщане на повърхността в разработка може да се зададе както чрез аналитични зависимости, така и чрез графичен алгоритъм.
Още в първите работи по дескриптивна геометрия бяха добре разработени алгоритми за конструиране на точни сканирания на цилиндър, конус и торс на хеликоид (отворена спирална повърхност). Под развитие на повърхнината се разбира съчетаването на част (отделение) от повърхнината с равнината. Част от цилиндъра се изрязва от един от генераторите и се подравнява с равнината. Развитието на страничната повърхност на прав кръгъл цилиндър се изобразява като правоъгълник с височинаlи дължинаπd, къдетоlе дължината на образуващата на цилиндричната повърхнина,dе диаметърът на основата на цилиндъра (фиг. 5.19).
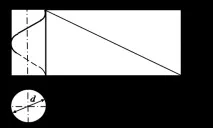
Ориз. 5.19. Разстъргване на прав кръгъл цилиндър
В допълнение към правите линии на огъване и усукване върху разработката могат да бъдат начертани много други прави линии, които на повърхността съответстват на геодезични линии, които определят най-късите разстояния между точките на повърхността. Нацилиндрични и конични повърхности, геодезическата линия е спирала.
Развитието на прав кръгъл конус е сектор от окръжност с радиусlи ъгълφ, равен на или2π∙cosβ, къдетоlе дължината на образуващата,dе диаметърът на основата на конуса (фиг. 5.20). Конусът и цилиндърът се разглеждат като частен случай на повърхност с извивка, когато извивката се изражда в крайна точка в безкрайност. Коничната повърхност също има два етажа, разположени от противоположните страни на върха на конуса.
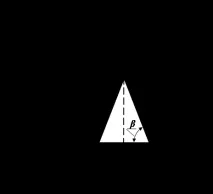
Ориз. 5.20. Развитие на прав кръгов конус
На фиг. 5.21 показва пример за изграждане на размах на един етаж на хеликоид, ограничен от обратен ръб (спирала - цилиндрична спирала с диаметърd), хоризонтални равнини с разстояние между тях, равно наh(височинаh). Повърхността се изрязва по ръба на издатината и един от генераторите и се подравнява с равнината. Спиралата на разработката се превръща в кръгова дъга с радиусρи ъгълφ. Дължината на кръговата дъга е равна на дължината на спиралата (L=π d/ cosβ). Стойността на радиусаρсе определя от равенството2 π ρ φ/360°= π d/ cosβ. Откъдетоρ = d 180°/ cosβ∙φ. Образуващите на хеликоида са успоредни на образуващите на насочващия конус, следователно сборът от ъглите между образуващите на хеликоида е равен на сбора от ъглите между насочващите конуси (φ = 2π∙cosβ). Ако вместоφзаместим неговата стойност, тогава получавамеρ = d / 2cosβ 2.
Повърхност с връщащ се ръб има два етажа, лежащи от противоположните страни на допирните точки. Ако обратният ръб е плоска извита линия, тогава повърхността се превръща в равнина.
На линейни повърхности с обща форма могат да се разграничат линии на компресия (гърлото на еднослоен хиперболоид, линиятастесняване на наклонената равнина, стрикционни линии на цилиндроида и др.), върху които се пресичат близките повърхнини на образуващата. Линиите на компресия са аналогични на връщащия ръб, с единствената разлика, че генераторите не докосват линията на компресия, а я пресичат под някакъв ъгъл. Цилиндрични, конични и издатини повърхности могат да бъдат получени от равнината на развитие чрез деформация на огъване. Линейни повърхности с обща форма се получават от равнината на развитие чрез деформация на усукване и огъване. Отбелязваме също, че е само теоретично възможно да се получи повърхност от равнината на развитие чрез огъване и на практика наличието на деформации на натиск и напрежение е неизбежно, тъй като няма продукти без дебелина.
 |
Ориз. 5. 21. Развитие на еволвентен (отворен) хеликоид
Развитието на повърхността на отделение на директен затворен хеликоид със стъпкаHи диаметър на цилиндрична спиралаdе непълен пръстен (фиг. 5.22). Стъпалото на спиралната повърхност се разгръща до дължината на дъгата на окръжност с диаметърd1, ТогаваН = π d1 ∙ φ/360°. Нека от получената зависимост определим стойността на ъгълаφ: φ= Н ∙360°/π d1. Тогава,L = πd/cosβ = π D ∙ φ/360°.D = d + d1. Заместете стойносттаDв предишния израз:L = πd/cosβ = π(d + d1) ∙ φ/360°. Нека определим стойността на ъгълаφ,φ=πd360°/cosβ(d + d1). Диаметърътd1може да се определи чрез сравняване на формулите за определяне на ъгълφ:d1 = Нd cosβ/(π 2 d – Нcosβ)илиd1 = d sinβ/(π –sinβ).

Ориз. 5.22. Развитие на прав затворен хеликоид
Развитие на повърхността на отделението на пръстеновиден затворен хеликоид сстъпкаHи диаметри на вътрешните и външните цилиндрични спирални линииdиd׳ също е непълен пръстен (виж Фиг. 5.22). Вътрешната спирала се разгръща до дължината на дъгата на окръжност с диаметърd׳. ТогаваL׳= πd/cosβ = π d׳∙ φ/360°. Нека определим стойността на ъгълаφ,φ=d360°/cosβ d׳. Външната спирала се разгъва до дължината на дъгата на окръжност с диаметърD. Тогава,L = πd/cosβ = π D ∙ φ/360°.D = (d - d׳) + d1. Заместете стойносттаDв предишния израз:L = πd/cosβ = π(d – d׳+ d1) ∙ φ/360°. Нека определим стойността на ъгълаφ,φ=d360°/cosβ(d – d׳+ d1).
Развитието на повърхността на отделение на наклонен затворен хеликоид е усукан пръстен, образуващите повърхности на развитието докосват кръг с определен радиус. Развитието на повърхността на отделение на еднослоен хиперболоид на въртене също е усукан пръстен, образуващите повърхности на развитието докосват кръг с някакъв радиус. Гърлото на повърхността се разгръща в дъга от окръжност на вътрешната дъга на окръжност, а основата на еднослоен хиперболоид се разгръща в дъга от окръжност на външната дъга на окръжност. За да се изгради разработка на линейчата повърхност, е необходимо да се знае законът за трансформация на водещите линии на повърхността в линии на равнината на разработка и законът за разпределение на прави линии, съответстващи на генераторите на повърхността. Законът за превръщане на повърхността в разработка може да се зададе както чрез аналитични зависимости, така и чрез графичен алгоритъм. Развитието на линейка се изгражда за един етаж от ограничена част от повърхността. Разделянето на повърхността на подове става по линията на компресия.
Ако закономерността на прехода от повърхността към развитието е неизвестна, тогаваизгражда се приблизително сканиране. За целта повърхнината се заменя с вписана или описана многостенна повърхнина и се конструира нейното развитие. Ако повърхността е разделена на много триъгълници, тогава методът се нарича триангулация. Изграждането на размах е свързано с определянето на естествения размер на всяко лице. Разгледаните в предходните лекции метрични задачи са неразделна част от конструирането на размах. Изграждането на размаха е сложна метрична задача, в която е важно рационално да се организират графичните конструкции, за да се постигне точност и скорост на изграждане.
За пресечен цилиндър и конус, както и за наклонени цилиндрични и конични повърхности и други повърхности се изграждат приблизителни разработки, тъй като въпросите за конструиране на разработки не са достатъчно проучени: необходимо е да се установи геометрична проекционна връзка между повърхностите и техните разработки.
Помислете за пример за конструиране на изместване на призма, използвайки метода на търкаляне и метода на нормалното сечение. Нека разрежем призмата по ръбаAA׳ и завъртим лицата й около ръбовете, докато съвпаднат с фронталната равнина, минаваща през ръбаAA׳ . ТочкиВ,В׳ ,СиС׳ по време на въртене се движат в равнини, перпендикулярни на ръбовете (фиг.5.23). От точкаA2начертайте дъга с радиусA1B1до пресечната точка с перпендикуляра отB2къмA2A2׳ и получетеВо. По същия начин получаваме останалите точки. Прикрепяме долната и горната основа и получаваме пълния размах на призмата. Нека срежем призмата с равнинатаα, перпендикулярна на ребрата, и да определим действителния размер на сечениетоA"B"C"׳,, например, като го подравним сπ1. Нормалното сечение се разгъва в права линияAoBoCo.
| C2׳ |

Ориз. 5.23. Наклонена призма
На практика за несчупени нелинейчати повърхности също се изграждат размахи, за това те се апроксимират от развиващи се повърхности (те се разбиват на части, които се заменят с равнини или развиващи се повърхности, т.е. около тях се вписват или описват няколко цилиндрични, конични или други повърхности) и след това за тях се изграждат сканирания. Полученото разгъване на цялата повърхност е условно, тъй като се състои от много отделни плоски фигури; за да се получи повърхност, те трябва да бъдат залепени заедно и отделните участъци да бъдат подложени на компресия и напрежение. Колкото по-голям е броят на преградите, толкова по-малки са парчетата, на които се разпада повърхността. Това е основната разлика между условното почистване и приблизителното.