Изграждане на регресионна линия въз основа на групирани данни
При голям брой наблюдения данните обикновено се групират според една или повече променливи. За изследване на зависимости е желателно да се използват интервали за групиране с еднаква ширина. Неравните интервали могат да доведат до изкривени регресии и погрешни заключения. При голям обем на изследваната популация е най-целесъобразно да се формират 9–10 интервала, равномерно запълнени с честоти. При малки обеми от населението няма смисъл да се групират данните. Оценките, изчислени върху групиран материал, се различават от оценките, изчислени върху негрупиран материал. Причината за това е в прехода при изчисленията към средата на интервалите и условно приетото равномерно разпределение на честотите по ширината на тези интервали. С голямо количество данни се смята, че неточностите в резултатите, дължащи се на групиране, са напълно изкупени чрез опростяване на процедурата за изчисление.
Тема 3. Множествен линеен регресионен модел
1. Определяне на параметрите на сдвоения модел на линейна регресия с помощта на метода на най-малките квадрати
2. Оценка на тясността на връзката между променливите
3. Оценка на качеството на регресионното уравнение
4. Предистория на метода на най-малките квадрати
Линейна множествена регресия
В действителност всяко явление се определя от действието не на една причина, а на няколко или по-скоро на цял комплекс от причини. Сложна комбинация от причини води до различни резултати. Например, действайки в една и съща посока, те засилват действието, действайки в противоположна посока, те взаимно се отслабват. Възниква въпросът за измерване на влиянието на комплекс от причини върху изследваното явление. Проблемът за изследване на зависимостта на една зависима променлива от няколко обяснителни променливиx1,x2, …,xmпри условия на определено време се решава с помощта на множествен или многовариантен регресионен анализ. Помислете за линейна връзка между променливатаyи обяснителните променливиx1,x2, …,xm.
Коефициентитеbk,k= 0, 1, 2, …,m се наричат регресионни параметри. Регресионната константаb0изпълнява функцията за изравняване в регресионното уравнение. Той определя пресечната точка на регресионната хиперповърхност с остаy. Стойноститеb1,b2, …,bmса оценки на регресионните коефициенти. Коефициентът на регресияbkизмерва средния частичен ефект от промяната на променливатаxk,k= 1, 2, …,m, като се приема, че останалите обяснителни променливи(x1,x2, …,xk-1,xk,xk+ 1, …,xm)остават непроменени на постоянно ниво. Следователно, от гледна точка на статистическата методология, няма разлика между множествена и частична регресия. Поради тази причина в литературата параметритеbk,k= 1, 2, …,m се наричат едновременно коефициенти на множествена и частична регресия. Но заключението, че за определяне на регресионните коефициенти е достатъчно да се дефинират няколко прости линейни регресииyнаxk,k= 1, 2, …,m е погрешно. За надеждни оценки са необходими методи за оценка, които вземат предвид многостранните връзки на съвместно зависимите променливи.Най-често използваният е двуетапният метод на най-малките квадрати, който е обобщение на метода на най-малките квадрати.
Помислете за първата линейна множествена регресия с две обяснителни променливи:
Методът на най-малките квадрати води до условието:
, където
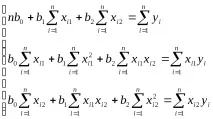
Получената система от нормални уравнения по отношение на неизвестни параметри може да бъде решена с помощта на формулите на Крамер.

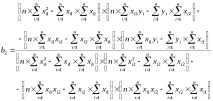
Множествените или частичните регресионни коефициенти могат да бъдат представени като вариации и ковариации:
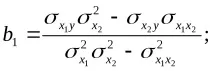
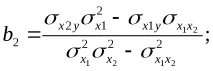
където
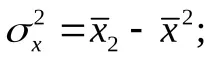
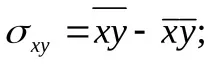
Изграждаме линейна множествена регресия на общата сума на данъците и плащанията върху общата сума на приходите от данък върху добавената стойност и данък общ доход (подоход).
y(общата сума на данъците и плащанията към консолидирания бюджет на Руската федерация), млрд. рубли
x1(общо постъпления от данък общ доход в консолидирания бюджет на България), млрд. рубли
x2(общо постъпления от ДДС в консолидирания бюджет на България), млрд. рубли