Как се измерва социалното неравенство - информационно-аналитичен портал ОКОТО НА ПЛАНЕТАТА

Справедливо ли са разпределени доходите на гражданите в държавата? Това може да се изчисли. От гледна точка на икономистите, колкото по-равномерно са разпределени парите, толкова по-справедливи са, а за определяне на равномерността отдавна са измислени два показателя - „коефициентът на децила” и „Коефициентът на Джини”.
Сега нека се задълбочим в материала.
== Децилен коефициент ==
Децил е, грубо казано, една десета.
Да кажем, че в нашата фабрика работят 500 души. Да помолим главния счетоводител да сортира всички служители по заплати и да ги подреди в един ред. Най-ляво в редицата ще бъде Дрихунов, пазачът с най-ниска заплата. Най-вдясно ще стои директорът на завода Топоногов.
Както е лесно да се изчисли, една десета от 500 души е 50 души. Първите 50 души (най-ниско платените, като се започне от портиера Дрихунов) са първият децил. Последните 50 души (най-високоплатените, затваряйки директора Топоногов) са десетият децил.
Сега разделяме общата заплата на десетия децил на заплатата на първия децил.
Да предположим, че общата заплата на първия децил е 500 хиляди рубли (средно 10 хиляди на служител). Да приемем, че общата заплата на последния децил е 4 милиона рубли (средно 80 хиляди рубли на служител). Разделяме 4 милиона на 500 хиляди, получаваме децилен коефициент 8. Това е показател за неравенство в нашия завод.
Такъв малък децилен коефициент - 8 - се наблюдава например в Армения и Дания. Това се счита за много добро представяне. Между другото, отбелязвам, че има нещо общо между Армения и Дания: те са малки държави и за малките страни е много по-лесно да поддържат относително равенство, отколкото за големите.
Можете да разгледате децилните коефициенти за другизаявява, ако сортирате тази таблица в Уикипедия по първата колона, по „R/P 10%“:
В тази ситуация „R / P 10%“ означава „10% от богатите към бедните“, „съотношението на доходите на най-богатите 10% към доходите на най-бедните 10%“.
Имайте предвид, че данните на ООН и ЦРУ за България се различават от данните на Росстат, нашият Росстат традиционно оценява ситуацията в страната по-песимистично от западните източници.
И така, според ООН и ЦРУ децилният коефициент в България за 2002 г. е 12,7 - 12,8, а според Росстат - 14.
Отбелязвам, че и 12,7, и 14 са доста добър показател за такава голяма страна като България. За сравнение, в Бразилия децилният коефициент е 50, в Китай - 22, в САЩ - 16. В малката Чехия е лесно да запазите същите заплати: можете да карате кола от край до край за няколко часа. В България пространствата са по-внушителни.
Може би сте забелязали, че таблицата на Wikipedia също има колона за R/P 20%. Това е така нареченото „квинтилно съотношение“, съотношението на доходите на най-богатите 20% към доходите на най-бедните 20%. Квинтилът, познахте, е приблизително една пета.
Росстат пуска отлична обобщена таблица, която показва историята на разпределението на доходите по квинтили в България от 1970 г. насам:
Същата таблица показва историята на децилния коефициент и историята на коефициента на Джини, за които ще пиша по-долу.
Любопитно е, че през 1970 г. квинтилното съотношение е 4,7. Това е много по-малко от сега (сега 9,1) и приблизително съответства на съвременните показатели на Швеция, Белобългария и Холандия.
Както можете да видите, децилният коефициент се счита за много прост, но има единзначителен проблем. А именно, когато изчисляваме децилния коефициент, ние не вземаме предвид заплатите на 80% от средноплатените служители.
Представете си две фабрики.
Завод номер 1 - 90% от персонала (работниците) получават по 10 хиляди рубли, 10% от персонала (ръководството) получават по 80 хиляди рубли. Децилен коефициент - 8.
Завод номер 2 - 10% от нископлатения персонал получават по 10 хиляди рубли, други 10% - по 20 хиляди рубли, по-голямата част от работниците - от 30 хиляди до 75 хиляди. 10% от ръководството получават по 80 хиляди рубли. Децилен коефициент - 8.
Ясно е, че ситуацията с равенството в двата завода е коренно различна. Но децилният коефициент не ни показва това.
== Индекс на Джини ==
(За педантите има малка разлика между "индекс" и "коефициент", индексът на Джини се разглежда като процент, а коефициентът на Джини е в дробни числа от нула до едно. Ще използвам тези термини като синоними, приемайки, че 43% и 0,43 са едни и същи).
Ето какво означава индексът Джини. Както предупредих, ще бъде трудно по-нататък, ще ви трябват знания по математика на ниво 7-ми клас на училището.
Представете си определена страна, в която всеки жител получава една и съща заплата, един долар на човек. Нека да изградим графика, върху която ще отразим заплатите на жителите на базата на начисляване, добавяйки ги един към друг:
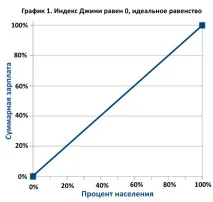
Това е напълно равно разпределение на заплатите. При изчисляване на индекса Джини се счита за идеален.
Сега, напротив, нека вземем пример, който е възможно най-далеч от идеала. Да речем у нас 1 човек получава милион долара заплата, а всички останали работят за него безплатно. Нека изградим графика на заплатите отново:
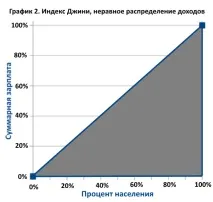
Големият сив триъгълник на графиката ее индексът на Джини. Отклонение от идеалното разпределение на доходите. Неравенството, показано на графика 2, е максималното, стойността на индекса Джини в такова състояние се приема за 100.
Както можете лесно да видите на графиката, площта на триъгълника, оцветен в сиво, е 50%. По този начин индексът на Джини е площта на зоната на отклонение от идеала, умножена по две.
Нека сега разгледаме малко картина на реалното разпределение на доходите. Да вземем например данните на Росстат за България за 2014 г. Той показва разпределението на доходите в пет квинтила, което е напълно достатъчно за груба оценка на коефициента на Джини:
Разпределение на доходите в България през 2014 г. :
Първи квинтил (0-20%): 5,2 Втори квинтил (20-40%): 9,9 Трети квинтил (40-60%): 14,9 Четвърти квинтил (60-80%): 22,6 Пети квинтил (80-100%): 47,4
За всеки случай ще дешифрирам тези данни. Ако съберем всички доходи на всички граждани в България на една купчина, то най-бедните 20% ще вземат 5,2% от тази купчина, а най-богатите 20% - 47,4%, почти половината.
Сега изграждаме графика, на която ще бъде възможно да изчислим неравенството в доходите. (За любопитните, тази графика се нарича крива на Лоренц, на името на друг икономист, но не е нужно да знаем това точно сега.)
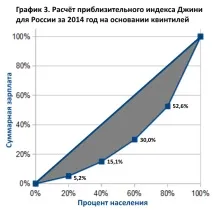
Как да изчислим площта на защрихована сива фигура?
За тези, които сега не са склонни да се ровят в алгоритъма за изчисление, препоръчвам да пропуснете текста, маркиран в цитата, за тези, които са свикнали да проверяват сами всички числа, казвам:
1. Да припомня разпределението на доходите по квинтили: 5.2%; 9,9%; 14,9%; 22,6%; 47,4%. 2. Нека обобщим цифрите на база начисляване: 5,2%; 15,1%; 30,0%; 52,6%; 100%. 3. Нека изградим графика. Както е лесно да се види, площта S, от която се нуждаем, се изчислява като площта на половин квадрат(50%) минус площта на фигури S1, S2, S3, S4 и S5:
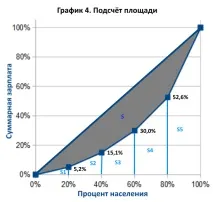
4. Площта на фигурата S1 е лесна за изчисляване - това е (20% * 5,2%) / 2 \u003d 0,52%. 5. Областта на фигура S2 се състои от правоъгълник и триъгълник отгоре. Площ на правоъгълник: 20% * 5,2% = 1,04%. Площ на триъгълника: ((15,1% - 5,2%) * 20%) / 2 = 0,99%. Обща площ на фигура S3: 1,04% + 0,99% = 2,03% 6. По същия начин изчисляваме площите на фигури S3, S4 и S5: 4,51%; 8,26%; 15,26%. 7. Вече сме готови да изчислим площта на защрихованата сива фигура S: 50% - 0,52% - 2,03% - 4,51% - 8,26% - 15,26% = 19,42%. 8. Умножаваме полученото число по две и това е желаният от нас индекс на Джини: 38,8.
И така, изчислихме индекса Джини за България за 2014 г. - той е 38,8. Сега нека сравним с цифрата на "Росстат", която публикува индексите Джини в същия файл, който вече споменах два пъти днес:
Росстат дава малко по-различна цифра - 41,6. Несъответствието се дължи на факта, че ние разделихме всички жители на България само на пет части, а Росстат, вероятно, ги разделя на 100 части, за да изчисли отделно всеки процент. В Росстат, разбира се, резултатите са по-точни.
Обобщаване
Освен това индексът Джини се изчислява за различни страни, така че можем да се сравним с други страни и да видим докъде сме се придвижили към премахване на несправедливите неравенства.
Поглеждайки назад към миналото, може да се види, че индексът на Джини, който в съветско време беше на нивото на малките, добре нахранени европейски страни, вече се е повишил до значителните 38,7 до 1995 г., а до 1999 г. е достигнал границата от 40,0.
Индексът достигна своя връх от 42,2 през 2007 г., но сега индексът леко се понижи до 41,6:

И накрая, нека ви напомня товалибералните митове за „чудовищното неравенство“ в България са подредени тук:
Може би за пълнота днес трябва да говоря и за неравенството между нашите региони. Но това е тема за отделен пост.