Класическата дефиниция на вероятността
Класическата дефиниция на вероятността.
1. Тесте от 32 карти е внимателно разбъркано. Намерете вероятността и четирите аса да лежат в тестето едно след друго, без да се разпръскват други карти.
Решение. Броят на всички възможни начини за подреждане на карти в тесте е 32! За да изчислите броя на благоприятните резултати, първо си представете, че четири аса са някак си подредени едно след друго и залепени заедно, така че да съставляват една карта (няма значение, че тя се оказа по-дебела от всички останали). Полученото тесте сега има 32 - 4 + 1 = 29 карти. Картите в това тесте могат да бъдат подредени по 29 начина! Броят на всички благоприятни резултати се получава, ако това число се умножи по 4! е броят на възможните начини за подреждане на четирите аса. От тук получаваме отговора на проблема: .
2.nигри се играят между двама играчи и всяка игра завършва или с победа, или със загуба, като всички възможни резултати от игрите са еднакво вероятни. Намерете вероятността определен играч да спечели точноmигри, 0 mn.
Решение. Всяка партия има два изхода - победа на единия или на другия участник. За две игри има 2 2 = 4 изхода, за три игри - 2 3 =8 изхода, заnигри - 2nизхода. Сред тях точно резултатите съответстват на печалбата на един от играчите вmигри. Следователно търсената вероятност е равна на .
3. Хвърлят сеnзара. Намерете вероятността всички зарове да имат еднакъв брой точки.
Решение. Общият брой резултати тук е 6n. Броят на благоприятните резултати е 6. Отговорът на задачата е:
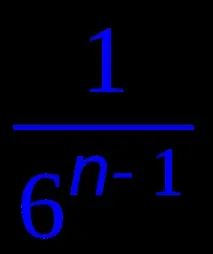
4. Урна съдържаaбели иbчерни топки (a2;b2). От урната се изтеглят 2 топки без подмяна. Намерете вероятността топките да са с еднакъв цвят.
Решение. Тази вероятност е
5. Урната съдържаaбели иbчерни топки. Топките без подмяна се изваждат от урната. Намерете вероятносттаk-тата изтеглена топка да е бяла.
Решение. Нека си представим процеса на произволно извличане на топки от урната по следния начин: топките се поставят произволно в клетките, разположени в редица, и се изваждат от клетките една по една отляво надясно. Тогава се получава благоприятен резултат, когатоk-та клетка съдържа бяла топка.
Общо възможно (a+b)! различни начини за подреждане на топки в клетки. Нека заемемk-та клетка с една от белите топки, което може да стане вaпо различни начини. Тогава останалите клетки могат да бъдат попълнени (a+b– 1)! начини и се оказва, че броят на благоприятните резултати е равен на (a+b– 1)!a, а желаната вероятност е
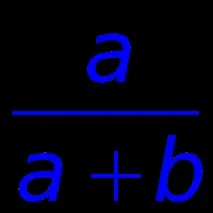
6. Намерете вероятността при поставяне наnразличими топки вNкутии, дадената кутия да съдържа точноk(0 kn) топки (всички различими поставяния са еднакво вероятни).
Решение. Първата топка може да бъде поставена поNразлични начина, втората топка поNразлични начина, а двете топки могат да бъдат поставени вNкутии поN2 начина. Общо имаNnопции за поставяне наnразличими топки вNкутии. Като изберете определена кутия, можете да намерите


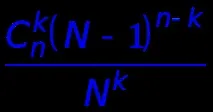
7. 10 букви от разделената азбука: A, A, A, E, I, K, M, M, T, T са произволно подредени в ред. Каква е вероятността да получите думата МАТЕМАТИКА?
Решение. 10 букви могат да бъдат подредени в редица по 10 начина! За да получите броя на благоприятните резултати, трябва да вземете думата MATH и да се уверите, че тя може да бъде получена чрез пренареждане на 3 букви A, 2 букви M и 2 букви T, което може да се направи 3!2!2! начини Отговор на задачата: 3!2!2!/10!.
8. Хвърлят се 10 зара. Приема се, че всички комбинации от изпуснати точки са еднакво вероятни. Намерете вероятността да падне поне една "6".
Решение. Общият брой резултати тук е 6 10 . Благоприятните резултати включват загуба на една, две, три и т.н. шестици. По-лесно е да се преброи броят на неблагоприятните резултати, т.е. резултатите, когато не е паднала нито една шестица. Очевидно има 5 10 от тях, а броят на благоприятните резултати е 6 10 - 5 10 . Желаната вероятност е равна на 1 - .
9. В една чанта има 10 различни чифта обувки. От чантата се изтеглят произволно 6 обувки. Намерете вероятността извадката да не включва две единици обувки, съставляващи един чифт.
Решение. Общият брой резултати е броят на възможните проби от 6 единици от общо 20 единици, тоест


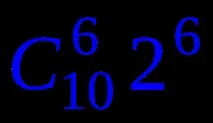

1.а. При условията на задача 1. изчислете вероятността, когато картите се раздават една по една в кръг на четирима играчи, всеки да получи по едно асо. (0,1055, )
1.б. В условията на предишната задача изчислете вероятността всички аса да отидат при един играч.
1.в.nлица се настаняват в редица в произволен ред. Каква е вероятността двама определени хора да са един до друг? Намерете съответната вероятност, ако едни и същи лица седнат на кръглата маса.
2.а. Решете задача 2. при условие, че всяка игра завършва с победа на един от участниците или с равенство и всички възможни резултати от игрите са еднакво вероятни.
2.б. Петима души са влезли в асансьора на 8-етажна сграда на първия етаж. Да предположим, че всеки от тях може да излезе с еднаква вероятност на всеки от етажите, като се започне от втория. Намерете вероятността и петте да излязат на различни етажи.
3.а. Хвърлят се шест зара. Намерете вероятността от следните събития:
а) различен брой точки се паднаха на всички зарове;
б) общият брой отпаднали точки е 7.
3.б. Намерете вероятността сред произволно избраните 12 души всички да имат рождени дни в различни месеци.
4.а. В условията на задача 4. намерете вероятността топките да са многоцветни.
5.а. В джоба има 10 ключа, от които само един става за тази ключалка, но не се знае кой. Ключовете се изваждат произволно от джоба един по един и се прави опит за отваряне на ключалката. Намерете вероятността ключалката да бъде отворена при 7-ия опит.
5 Б. Студентът Иванов, докато се готви за изпита, от 30 билета научи само 20. Група студенти на изпитсе състои от 16 човека, като всеки от своя страна взима по един билет без да го връща. В кой случай студентът Иванов е по-вероятно да издържи изпита: дали ще бъде първи в тази опашка или ако ще бъде последен?
5.в. Партида от 25 устройства съдържа едно дефектно устройство. От тази партида бяха избрани на случаен принцип 6 устройства за контрол. Намерете вероятността дефектното устройство да бъде включено в извадката.
5.g. Кутията съдържа 90 изправни и 10 дефектни винта. Ако използвате 10 винта, каква е вероятността никой от тях да не е дефектен? Каква е вероятността сред тях да има 4 дефектни винта?
6.а. Вnкутии поставетеnтопки, така че за всяка топка да е еднакво възможно да ударите всяка кутия. Намерете вероятността нито една кутия да не е празна.
6.б. Всяка отnпръчици се счупва на две части - дълга и къса. След това 2nфрагмента се комбинират вnдвойки, всяка от които образува нова "пръчка". Намерете вероятността а) частите да бъдат свързани в първоначалния ред; б) всички дълги части ще бъдат свързани с къси.
6.c. За да се намали общият брой игри, 2nотбора състезатели се разделят на две подгрупи. Определете вероятността двата най-силни отбора да бъдат: а) в различни подгрупи, б) в една и съща подгрупа. Отговор: а)n/(2n-1); б) (n–1)/(2n-1);
7.а. От буквите на раздвоената азбука е съставена думата СТАТИСТИКА. След това 5 букви се избират на случаен принцип от тези букви без замяна. Намерете вероятността избраните букви да образуват думата ТАКСИ. Отговорът е 2/21.
8.а. Каква е вероятността две хвърляния на три зара да дадат един и същ резултат, ако а) заровете са различими, б) заровете са неразличими.Отговор: 1/216; 83/3888.
8.б. От 28 домино две са избрани на случаен принцип. Намерете вероятността те да образуват „верига“ според правилата на играта. Отговор: 7/18.
8.в. Хвърлят се 10 зара. Намерете вероятността за следните събития: а) да са паднали точно 3 шестици, б) да са се паднали поне две шестици.
9.а. Двама играчи хвърлят независимо (всеки свои) монети. Намерете вероятността следnхвърляния те да имат еднакъв брой гербове. Отговор:

Решение на задача 1.а.
1-ви начин. При разбъркване на тесте карти в него могат да се поставят 32! различни начини. Първият играч ще получи асо от определен цвят (например асо пика), ако това асо е на 1-во, 5-то, 9-то и т.н. места в тестето. С други думи, асото пика отива при първия играч, ако той заема една от осемте възможни позиции в тестето. По същия начин, друго асо, например от боята на купа, отива при втория играч, ако той е втори, шести, десети и т.н. в тестето, тоест той също заема една от осемте възможни позиции в тестето. Разсъждавайки по подобен начин, получаваме, че за да се изпълни условието на задачата, картите в тестето трябва да се намират в една от 8 4 4!28! възможни начини. От това следва, че желаната вероятност е равна на
2-ри начин. Нека разделим тестето на 4 части по 8 карти всяка. Това може да се направи по няколко начина, равни на . Първата от тези части, при условие че съдържа едно и само едно асо, например асо пика, може да бъде съставено по няколко начина, равни на . Втората част, при условие че я удари едно асо, може да бъде съставена по няколко начина, равни на . По този начин е възможно да се раздели колодата на 4 части, които удовлетворяват условието на задачата по редица начини, равни на . От това следва, че желаната вероятност е равна на
111. Когато играете покерОт тесте от 52 карти на играча се дават 5 карти. Каква е вероятността играчът да получи комбинация от една тройка (три карти с една и съща номинация) и една двойка (две карти с една и съща номинация). (Тази комбинация се наричафул хаус).
112. В условията на предишната задача изчислете вероятността играч да получи една двойка, две двойки.
113. В условията на проблем 111 изчислете вероятността играчът да получи комбинациянаправо, тоест пет карти от поредна номинация, но не всички от същия костюм (например 5 от клубове, 6 от пика, 7 от клубове, 8 от сърца, 9 от диаманти или джак от пити, кралица на пикас, крал на Spades, Ace of Hearts, два от клубовете)
; ; .