Концепцията за фрактално измерение
L
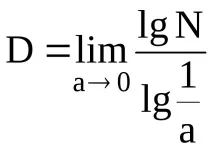
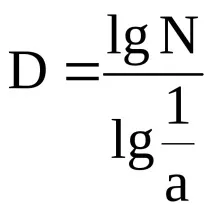
N – брой сегменти, размера.
D - "степен на огъване"
K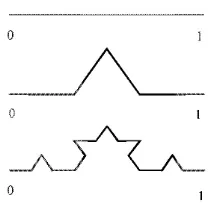
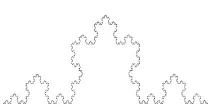
Фрактално измерение на множеството
Обемът на фрактал в неговотопространство за вгражданевинаги е равен на нула. Въпреки това, той може да бъде различен от нула в пространство с по-ниско измерение. За да определим размерността на това пространствоD, нека разделим цялотоn-мерно пространство на малки кубчета с дължина на ръбаεи обемεn— фиг.1. НекаN(ε) е минималният брой кубчета, които заедно напълно покриват фракталното множество, тогава по дефиниция
Това количество обикновено се наричаХаусдорфилифракталноизмерение.
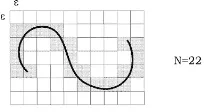
Фиг. 1.Как да намеря фракталното измерение?
Съществуването на тази граница означава, че обемът на фрактала вD-измерното пространство е краен: за малкиε
къдетоV=const. По този начин,N(ε) не е нищо друго освен броя наD-измерните кубове, които покриват обемаVвD-измерното пространство. Тъй катоn-мерните кубове, покриващи фрактала, може да се окажат почти празни
За гладък линеен сегмент с дължинаL:N(ε) =L/εи следователноD= 1. За площадкаSдвуизмерна повърхност:N(ε) =S/ε2 иD= 2 и т.н.
Рекурсивен алгоритъм за конструиране на конструктивни фрактали.
Триъгълник на Сиерпински

Триъгълникът на Серпинские фрактал, един от двумерните аналози на набора на Кантор, предложен от полския математик Серпински през 1915 г. Известен също като "решетката" на Сиерпински или "салфетката".
Сграда
е взетоплътен равностранен триъгълник, при първата стъпка вътрешността на медианния триъгълник се отстранява от центъра. На втората стъпка три медианни триъгълника се премахват от трите останали триъгълника и т. н. След безкрайно повтаряне на тази процедура остава подмножество от плътния триъгълник - триъгълникът на Серпински.
Конструкция на триъгълника на Серпински
Триъгълникът на Серпински може да бъде получен и чрез следния алгоритъм:
Вземете три точки на равнината и нарисувайте триъгълник.
Произволно изберете всяка точка вътре в триъгълника и преместете половината разстояние от тази точка до който и да е от трите върха на триъгълника.
Маркирайте текущата позиция.
Повторете от стъпка 2.
Триъгълникът на Серпински е затворен.
Триъгълникът на Серпински има топологична размерност 1.
има междинна (т.е. не цяло число) размерност на Хаусдорф. В частност,
има нулева мярка на Лебег.
Триъгълникът на Серпински се получава от триъгълника на Паскал чрез третиране на четните числа като точки, принадлежащи на триъгълника на Серпински, а нечетните числа като непринадлежащи.