Кратки теоретични сведения за аксонометричните проекции
Кратка теоретична информация за аксонометричните проекции - раздел Полиграфия, Учебно-методическо ръководство за изпълнение на графични произведения, модул № 5. Проекционен чертеж, аксонометрия и наклонен Комплексен чертеж, съставен от две или три проекции, O.
Сложен чертеж, съставен от две или три проекции, притежаващи свойствата на обратимост, простота и т.н., в същото време има значителен недостатък: липсва видимост. Ето защо, за да се даде по-визуално представяне на предмета, заедно със сложен чертеж се дава аксонометричен чертеж, който се използва широко при описание на дизайна на продукта, в ръководствата за работа, в монтажните схеми, за обяснение на чертежи на машини, механизми и техните части.
Сравнете две изображения - ортогонален чертеж и аксонометричен чертеж на същия модел. Кое изображение улеснява четенето на формуляра? Разбира се на аксонометричното изображение. (фиг.10.1)
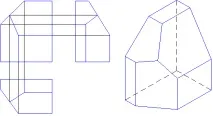
Същността на аксонометричната проекция е, че геометрична фигура, заедно с осите на правоъгълни координати, към които се отнася в пространството, се проектира паралелно върху определена проекционна равнина, наречена аксонометрична проекционна равнина или картинна равнина.
Ако отделим отсечкатаl (lx,ly,lz) върху координатните осиx,yиzи я проектираме върху равнинатаП¢, ще получим аксонометрични оси и отсечкиl'x, l'y, l'zвърху тях (фиг. 10.2)
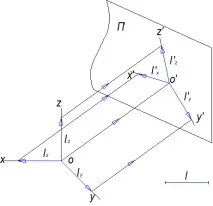
lx, ly, lz- естествени мащаби.
l'x, l'y, l'z- аксонометрични скали.
Полученият набор от проекции върху П¢ се нарича аксонометрия.
Съотношението на дължината на сегментите от аксонометричния мащаб към дължината на сегментите от естествения мащаб се нарича индикатор или коефициент на изкривяване по осите,които се означават сКx, Ky, Kz.
Kx= ;
Ky= ;
kz=
Видовете аксонометрични изображения зависят от:
1. От посоката на проектиращите лъчи (те могат да бъдат перпендикулярниП'- тогава аксонометрията ще се нарича ортогонална (правоъгълна) или разположена под ъгъл, не равен на 90 ° - наклонена аксонометрия).
2. От позицията на координатните оси към аксонометричната равнина.
Тук са възможни три случая: когато и трите координатни оси сключват остри ъгли (равни и неравни) с равнината на аксонометричната проекция и когато една или две оси са успоредни на нея.
В първия случай се прилага само правоъгълна проекция,(s ^ П')във втория и третия - само наклонена проекция(s П').
Ако координатните осиОХ, ОY,OZне са успоредни на равнината на аксонометричната проекцияП', ще се проектират ли върху нея в пълен размер? Разбира се, че не. Изображението на линиите в общия случай винаги е по-малко от естествения размер.
Разгледайте ортогонален чертеж на точкаAи нейното аксонометрично изображение.
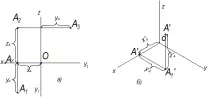
Позицията на точката се определя от три координати -XA, YA, ZA, получени чрез измерване на връзките на естествената полилинияOAX - AXA1 - A1 A(фиг. 10.3).
A'- основната аксонометрична проекция на точкатаA;
А- вторична проекция на точкаА(точкова проекция на проекция).
Коефициентите на изкривяване по оситеX', Y' и Z'ще бъдат:
kx= ;ky= ;ky=
В ортогоналната аксонометрия тези показатели са равни на косинусите на ъглите на наклона на координатните оси към аксонометричната равнина и следователно винаги са по-малки от единица.
Те са свързани с формулата
В наклонена перспективаиндикаторите за изкривяване са свързани с формулата
тези. всеки от тях може да бъде по-малък, равен или по-голям от единица (тук a е ъгълът на наклона на проектиращите лъчи спрямо аксонометричната равнина). И двете формули са производни от теоремата на Полке.
Теорема на Полке: аксонометричните оси на равнината на чертежа (П¢) и мащабите върху тях могат да бъдат избрани съвсем произволно.
(Следователно, аксонометричната система (O' X' Y' Z') обикновено се определя от пет независими параметъра: три аксонометрични скали и два ъгъла между аксонометричните оси).
Ъглите на наклона на естествените координатни оси спрямо равнината на аксонометричната проекция и посоката на проекцията могат да бъдат избрани произволно, следователно са възможни много видове ортогонални и наклонени аксонометрии.
Те са разделени на три групи:
1. И трите показателя за изкривяване са еднакви (kx = ky = kz). Този тип аксонометрия се наричаизометрия. 3k 2 =2; k=» 0,82 - теоретичен коефициент на изкривяване. Съгласно GOST 2.317-70 можете да използвате K=1 - намален коефициент на изкривяване.
2. Всеки два показателя са равни (например kx=ky kz). Този тип аксонометрия се наричадиметрия. kx=kz; ky = 1/2kx 2; kx 2 + kz 2 + ky 2 /4 = 2; k = » 0,94; kx = 0,94; ky = 0,47; kz = 0,94 - теоретични коефициенти на изкривяване. Съгласно ГОСТ 2.317-70 могат да се дадат коефициентите на изкривяване - kx=1; ky=0,5; kz=1.
3. 3. И трите показателя са различни (kx ¹ ky ¹ kz). Този тип аксонометрия се наричатриметрия.
На практика се използват няколко вида както правоъгълна, така и наклонена аксонометрия с най-простите връзки между индикаторите за изкривяване.
Тази тема принадлежи към раздела:
Учебно-методическо ръководство за изпълнение на графикаработи модул №5. Проекционен чертеж, аксонометрия и наклон
Държавен университет в Толиати, Автомобилен институт Катедра по дескриптивна геометрия и чертане..
Какво ще правим с получения материал:
Всички теми в този раздел:
Основни разпоредби Изображенията в чертежите, в зависимост от съдържанието, са разделени на изгледи, секции, секции в съответствие с GOST 2.305-68 *. По метода се получават изображения на обекти в чертежите
Основният изглед е този, който дава най-пълна представа за формата и размера на обекта Броят на изображенията трябва да е най-малък, но осигуряващ пълна представа за формата и размера на обекта. Ако основните изгледи са разположени в проекционна връзка, тогава техните имена не са за
Построяване на разрези На Фиг.3.1 са дадени три вида обект (без разрез). На основния изглед вътрешните повърхности: правоъгълен жлеб и цилиндричен стъпаловиден отвор са показани с пунктирани линии.
Обозначаване на сеченията За да се знае на кое място обектът има формата, показана на изображението на сечението, се обозначават мястото, където е минавала сечещата равнина и самото сечение. Линия, обозначаваща se
Щриховка на материали в разрези и разрези В разрези и разрези фигурата, получена в сечещата равнина, е щрихована. GOST 2.306-68 установява графично обозначение на различни материали (фиг. 3.4)
Вертикален разрез е разрез с режеща равнина, перпендикулярна на хоризонталната равнина на издатините.
Локален разрез е разрез, който служи за избистряневътрешната структура на обект само в отделно ограничено място В машиностроенето при изчертаване на плътни (некухи) обекти не се използват пълни разрези. Въпреки това, често има локални вдлъбнатини или дупки в твърди части, чиято форма трябва да бъде показана.
Връзката на част от изгледа и част от разреза Формата на много обекти е такава, че при изобразяването им не е достатъчно да се даде само разрез, тъй като понякога е невъзможно да се представи външната форма на обект от разрез. При изобразяване на такива
Разрез, получен с помощта на няколко режещи равнини, се нарича сложен Сложните разрези са начупени, ако режещите равнини се пресичат (фиг. 3.18) и стъпаловидни, ако режещите равнини са успоредни една на друга (фиг. 3.19) За
Конструкция на секции Фиг.4.1 показва вал с две плоскости (плоски изрези от двете страни) и шпонков канал (правоъгълна вдлъбнатина с полукръгли краища, предназначени за шпонка). Какво
Разположение на секциите В зависимост от местоположението на секциите те се разделят на разширени и насложени. Подробни участъци се наричат тези, които са разположени извън контурите на изображението.
Разликата между разрез и разрез Разрезът се различава от разреза по това, че разрезът показва какво се намира в сечещата равнина и какво се намира зад нея, а разрезът показва само това, което не е
Обозначаване на разрези Разрезите в чертежите са обозначени по същия начин като разрезите. Режещата равнина е показана като празна линия. Всяка равнина е обозначена едновременно в началото и в края
Някои правила за построяване на сечения При няколко еднакви сечения, свързани с един и същ обект, линиите на сеченията трябва да бъдат маркирани с една и съща буква и да бъде начертано едно сечение (фиг. 4.8). &nb
Конвенции и опростявания, използвани при изпълнението на изображения При изпълнение на различни изображения се използват конвенции и опростявания, които намаляват обема на графичната работа, като същевременно запазват яснотата и яснотата на изображенията на обекти.
Призма Фиг. 8.1 Даден е тристен
Пирамида Дадена е пресечена тристенна пирамида Ф(S,АВС) (фиг.8.2). Тази пирамида F се пресича от равнини S, D и G. 2 GPZ, 2 алгоритъм (Модул
Тела, ограничени от повърхности на въртене Телата на въртене са геометрични фигури, ограничени от повърхности на въртене (топка, елипсоид на въртене, пръстен) или повърхност на въртене и една или повече равнини (
Цилиндър на въртене Ако оста на въртене е перпендикулярна на P1, тогава цилиндърът ще се проектира върху тази равнина като кръг, а върху другите две проекционни равнини като правоъгълници
Конус на въртене Задачите на фигури 8.8, 8.9, 8.10, 8.11, 8.12 -2 GPZ (модул № 3) се решават съгласно 2-ри алгоритъм, тъй като повърхността на конуса не може да бъде проективна, а секущите равнини са челни навсякъде
Правоъгълна изометрия При изометрията всички оси са наклонени спрямо аксонометричната равнина под един и същ ъгъл, следователно ъгълът между осите (120°) и коефициентът на изкривяване ще бъдат еднакви. Избор на мащаб
Изометрия на кръга Кръговете се проектират върху проекционната равнина в пълен размер, когато са успоредни на тази равнина. И тъй като всички равнини са наклонени към аксонометричната равнина, околните
Етапи на изпълнение на визуално представяне на детайла 1. Частта се вписва в повърхността на четириъгълна призма, чиито размери са равни на общите размери на частта. Тази повърхност се нарича обвивка. Изометрия в ход
Правоъгълен диметрий Правоъгълна диметрична проекция може да се получи чрез завъртане и накланяне на координатните оси спрямо P¢, така че индикаторите за изкривяване по осите X' и Z'
Построяване на кръгове в правоъгълна диметрия Кръговете, лежащи върху координатни равнини в правоъгълна диметрия, както и в изометрия, ще бъдат показани като елипси. Елипси, разположени на равнините между осите
Наклонена диметрична проекция (фронтална) Ако координатните оси X и Y са успоредни на равнината P¢, тогава индикаторите за изкривяване по тези оси ще станат равни на единица (k = m = 1). Индикаторът е изкривен
Наклонени сечения Когато се правят чертежи на машинни части, често е необходимо да се използват наклонени сечения. При решаването на такива проблеми е необходимо преди всичко да се разбере: как трябва
Библиографски списък 1. Суворов, С. Г. Инженерен чертеж във въпроси и отговори: (справочник) / С. Г. Суворов, Н. С. Суворова.-2-ро изд. ревизиран и допълнителни - М.: Машиностроене, 1992.-366s. 2. Федо