lab_fraktaly - lab fractals - lab2 - Bresenham2
Алгоритъм за изчертаване на права линия
Тъй като екранът на растерния дисплей с електроннолъчева тръба (CRT) може да се разглежда като матрица от отделни елементи (пиксели), всеки от които може да бъде осветен, не е възможно директно да се начертае сегмент от една точка до друга. Процесът на определяне на пикселите, които най-добре се доближават до даден сегмент, се нарича растеризация. Когато се комбинира с процеса на прогресивно рендиране на изображение, той е известен като преобразуване на растерно сканиране. За хоризонтални, вертикални и наклонени 45°. сегменти, изборът на растерни елементи е очевиден. За всяка друга ориентация е по-трудно да изберете желаните пиксели, както е показано на фиг. 1.
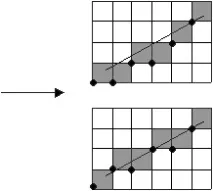
Фиг.1.1. Разлагане в растер от сегменти.
Общите изисквания към алгоритмите за чертане на сегменти са следните: сегментите трябва да изглеждат прави, да започват и завършват в дадени точки, яркостта по сегмента трябва да е постоянна и да не зависи от дължината и наклона, трябва да рисувате бързо.
Постоянна яркост по целия сегмент се постига само при рисуване на хоризонтални, вертикални и наклонени под ъгъл от 45 ° прави линии. За всички останали ориентации растеризирането ще доведе до неравномерна яркост, както е показано на фиг. 1.
Повечето алгоритми за чертане на линии използват алгоритъм стъпка по стъпка за опростяване на изчисленията. Ето пример за такъв алгоритъм:
Прост алгоритъм стъпка по стъпка
1. Позицияако - край крайтогава 2
позицияако
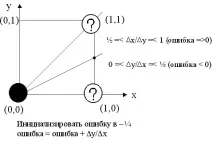
Ориз. 3.1. Основната идея на алгоритъма на Bresenham.
Не всички сегменти преминават през точките на растера. Подобна ситуация е илюстрирана на фиг. 3.2, където сегмент с наклон 3/8 първо преминава през растерната точка (0,0) ипоследователно пресича три пиксела. Също така е илюстрирано изчисляването на грешката при представяне на сегмент чрез отделни пиксели.
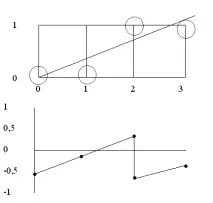
Фиг.3.2. Графика на грешката в алгоритъма на Bresenham.
Тъй като е желателно да се проверява само знака на грешката, той първоначално е зададен на -1/2. Така, ако наклонът на сегмента е по-голям или равен на 1/2, тогава стойността на грешката в следващата растерна точка с координати (1,0) може да се изчисли като
където m е наклонът. В нашия случай с начална стойност на грешката -1/2
Тъй като e е отрицателно, сегментът ще премине под средата на пиксела. Следователно пиксел на същото хоризонтално ниво по-добре приближава позицията на линейния сегмент, така че y не се увеличава. По същия начин изчисляваме грешката
на следващия пиксел (2,0). Сега e е положително, така че сегментът ще премине над средната точка. (2,1) растерният елемент със следващата по големина y-координата по-добре приближава позицията на сегмента. Следователно y се увеличава с 1. Преди да разгледаме следващия пиксел, е необходимо да коригираме грешката, като извадим 1 от него.
Обърнете внимание, че пресечната точка на вертикалната линия x \u003d 2 с дадения сегмент се намира 1/4 под линията y \u003d 1. Ако преместим сегмента 1/2 надолу, получаваме точно стойността -3/4. Продължаването на изчислението за следващия пиксел дава
Тъй като e е отрицателно, y не нараства. От всичко казано следва, че грешката е интервалът, отрязан по оста y от въпросния сегмент във всеки растерен елемент (спрямо -1/2).
Ето алгоритъма на Bresenham за първи октант, т.е. за случая 0 = 0 )
Блоковата схема на алгоритъма е показана на фигура 3.3. Пример е показан по-долу.
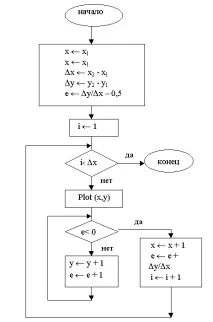
Ориз. 3.3. Блок-схема на алгоритъма на Bresenham.
Пример 3.1.Алгоритъм на Bresenham.
Помислете за сегмент, начертан от точка (0,0) до точка (5,5). Разлагането на сегмент в растер с помощта на алгоритъма Bresenham води до следния резултат:
резултатите от стъпковия цикъл
Резултатът е показан на фигура 3.4 и е според очакванията. Имайте предвид, че растерната точка с координати (5,5) не е активирана. Тази точка може да се активира чрез промяна на цикъла for-next от 0 до x. Активирането на точка (0,0) може да бъде елиминирано чрез поставяне на оператора Plot непосредствено преди реда, следващ i.
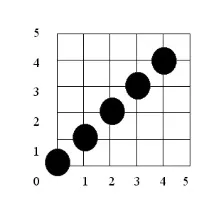
Ориз. 3.4. Резултатът от алгоритъма на Bresenham в първия октант.
Следващият разделописва общия алгоритъм на Bresenham.
4. Общият алгоритъм на Bresenham.
За да бъде пълно изпълнението на алгоритъма на Bresenham, е необходимо да се обработят сегменти във всички октанти. Модификацията е лесна за изпълнение, като в алгоритъма се вземе предвид номерът на квадранта, в който се намира сегментът и неговият наклон. Когато абсолютната стойност на наклона е по-голяма от 1, y постоянно се променя с единица и критерият за грешка на Bresenham се използва, за да се реши дали да се промени стойността на x. Изборът на постоянно променяща се (с +1 или -1) координата зависи от квадранта (фиг. 4.1.). Общият алгоритъм може да се формулира по следния начин:
Обобщен алгоритъм на квадранта на Bresenham с цяло число
приема се, че краищата на отсечката (x1,y1) и (x2,y2) не съвпадат
всички променливи се третират като цели числа
Sign - функция, която връща -1, 0, 1 съответно за отрицателен, нулев и положителен аргумент
s1 =Знак (x2 - x1)
s2 =Знак (y2 - y1)
обмен на стойности x и y в зависимост от наклона на сегмента
ако y 0)
ако Размяна = 1тогава
друго
край ако
край докато
ако Размяна = 1тогава
друго
край ако
следващ i
завършете
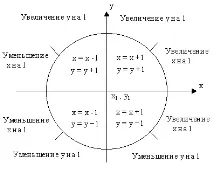
Фиг.4.1. Анализ на случаи за обобщения алгоритъм на Bresenham.
Пример 4.1. обобщен алгоритъм на Bresenham.
За илюстрация разгледайте сегмент от точка (0,0) до точка (-8, -4).
резултатите от стъпковия цикъл
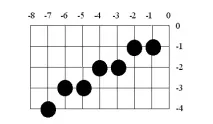
Фиг.4.2. Резултатът от работата на обобщения алгоритъм на Bresenham в трети квадрант.
На фиг. 4.2 показва резултата. Сравнение с фиг. 2.2 показва, че резултатите от двата алгоритъма са различни.
Следващият раздел обсъжда алгоритъма на Bresenham за генериране на кръг.
Алгоритъмът на Bresenham за генериране на кръг.
В растер е необходимо да се разложат не само линейни, но и други, по-сложни функции. Разлагането на конични сечения, тоест кръгове, елипси, параболи, хиперболи, е посветено на значителен брой произведения. Най-голямо внимание, разбира се, се отделя на обиколката. Един от най-ефективните и лесни за разбиране алгоритми за генериране на кръгове се дължи на Bresenham. Първо имайте предвид, че трябва да генерирате само една осма от кръга. Останалите части от него могат да бъдат получени чрез последователни отражения, както е показано на фиг. 5.1. Ако се генерира първият октант (от 0 до 45° обратно на часовниковата стрелка), тогава вторият октант може да бъде получен чрез огледално отразяване около правата линия y = x, което заедно дава първия квадрант. Първият квадрант е огледален около правата x = 0, за да се получи съответната част от кръга във втория квадрант. Горният полукръг се отразява спрямо правата линия y = 0, за да завърши конструкцията. На фиг. 5.1 са даденидвумерни матрици на съответните трансформации.
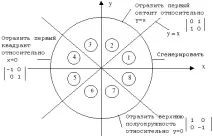
Ориз. 5.1. Генериране на пълен кръг от дъга в първия октант.
За да изведете алгоритъма, разгледайте първата четвърт от окръжност, центрирана в началото. Обърнете внимание, че ако алгоритъмът започва в точкатаx = 0, y = R,, тогава при генериране на кръг по посока на часовниковата стрелка в първия квадрант,yе монотонно намаляваща функция на аргументите (фиг. 5.2). По същия начин, ако началната точка еy =0,x==R,тогава при генериране на окръжност обратно на часовниковата стрелка,xще бъде монотонно намаляваща функция на аргументаy. 2> Приема се, че центърът на окръжността и началната точка са точно в точките на мрежата.
За всяка дадена точка от кръга, когато се генерира по посока на часовниковата стрелка, има само три възможности за избор на следващия пиксел, който най-добре се доближава до кръга: хоризонтално надясно, диагонално надолу и надясно, вертикално надолу. На фиг. 5.3 тези посоки се обозначават съответно с mH, mD, mV.
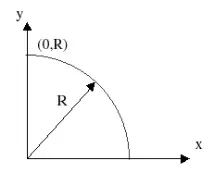
Фиг. 5.2. Кръг в първия квадрант.