Лекция 6 Аксонометрични проекции
Лекция 6
1. Общи сведения за аксонометричните проекции.
2. Класификация на аксонометричните проекции.
3. Примери за конструиране на аксонометрични изображения.
1 Въведение в аксонометричните проекции
При изготвянето на технически чертежи понякога става необходимо, заедно с изображения на обекти в системата от ортогонални проекции, да има повече визуални изображения. За такива изображения се използва методът на аксонометричната проекция (аксонометрия е гръцка дума, в буквален превод означава измерване по осите; аксон - ос, metreo - измервам).
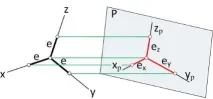
Същността на метода на аксонометричната проекция: обект, заедно с осите на правоъгълни координати, към които се отнася в пространството, се проектира върху определена равнина, така че нито една от неговите координатни оси не се проектира върху него в точка, което означава, че самият обект се проектира върху тази проекционна равнина в три измерения.
Мамка му. 88 върху определена равнина на проекции P се проектира разположена в пространството координатна система x, y, z. Проекции x p , y p ,
z p координатните оси в равнината P се наричат аксонометрични оси.
На координатните оси в пространството са нанесени равни отсечки e. Както се вижда от чертежа, техните проекции e x, e y, e z върху равнината P най-общо
случай не са равни на сегмента e и не са равни помежду си. Това означава, че размерите на обекта в аксонометричните проекции по трите оси са изкривени. Промяната на линейните размери по осите се характеризира с показатели (коефициенти) на изкривяване по осите.
Индексът на изкривяване е отношението на дължината на сегмент върху аксонометричната ос към дължината на същия сегмент върху съответната ос на правоъгълна координатна система в пространството.
Индексът на изкривяване по оста x ще бъде означен с буквата k, по оста y
- буквата m, по оста z - буквата n, след това: k = e x / e; m = e y /e; n = e z /e.
Големината на показателите за изкривяване и съотношението между тях зависи от местоположението на проекционната равнина и от посоката на проекцията.
В практиката на конструиране на аксонометрични проекции обикновено се използват не самите коефициенти на изкривяване, а някои стойности, пропорционални на стойностите на коефициентите на изкривяване: K: M: N = k: m: n. Тези стойности се наричат намалени коефициенти на изкривяване.
2 Класификация на аксонометричните проекции
Целият набор от аксонометрични проекции е разделен на две групи:
1 Правоъгълни проекции - получават се с посока на проекцията, перпендикулярна на аксонометричната равнина.
2 Наклонени проекции - получават се при избрана посока на проекция под остър ъгъл спрямо аксонометричната равнина.
В допълнение, всяка от тези групи също е разделена според съотношението на аксонометричните скали или показателите (коефициентите) на изкривяване. На тази основа аксонометричните проекции могат да бъдат разделени на следните видове:
а) Изометрични - индикаторите за изкривяване и за трите оси са еднакви (isos - еднакви).
б) Диметрични - показателите за изкривяване по две оси са равни една на друга, а третата не е равна (ди - двойна).
в) Триметрични - показателите за изкривяване и по трите оси не са равни
нас помежду си. Това е аксонометрия (тя няма голямо практическо приложение).
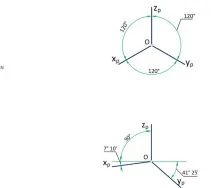
2.1 Правоъгълни аксонометрични проекции
Правоъгълен изометричен изглед
В правоъгълна изометрия всички коефициенти са равни между
k \u003d m \u003d n, k 2 + m 2 + n 2 \u003d 2,
тогава това равенство може да бъдезапишете във формата 3k 2 =2 , откъдето k = .
Така в изометрията индексът на изкривяване е равен на
0,82. Това означава, че в правоъгълен
изометрия, всички размери на изобразения обект са намалени с 0,82 пъти. За