Математика за деца
Щрихи.
За малки деца такива задачи са упражнения за твърдост на ръцете и внимание. Те могат да се дават веднага след като детето се научи съзнателно да държи молив в ръцете си. Разбира се, трудността може да се увеличи с времето. За по-големите деца това по същество е само една математическа задача. Но преди да вземете решение, трябва да пораснете. Ето защо има смисъл да се връщаме към тези задачи от време на време, като проверяваме дали е време да зададем този основен въпрос -в какви случаи е възможно и в кои е невъзможно контурът да се очертае с една линия?
Задача 1 Очертайте картината (Фиг. 1 ), без да вдигате химикала от хартията и без да преминавате два пъти над която и да е линия.
Ако просто не е интересно да го направите, можете да добавите антураж. Например: стар планински спасител (или пътник) трябва да минава през всички пътеки всяка вечер, да проверява дали някой се е загубил, дали се е загубил. . . Уморява се от дългия път; трябва да му помогнете, като направите план за обход.
За да свикнат децата, може да имате нужда от много такива снимки. Много е лесно да ги нарисувате. Не е необходимо картината да е симетрична, достатъчно е само да нарисувате затворена разбъркана "драскулка-драскулка" или да пресечете колкото искате затворени фигури.
Би било добре да контролирате решаването на проблемите (и да не вярвате на думата „Направих го“): дори възрастен може да се обърка и да се заблуди, ако кръгне доста трудна картина без контрастен молив. С малки деца най-вероятно ще трябва да седнете един до друг. На по-големите деца може да се предложи да номерират кръстовища и да запишат числата "по посока на движение".
На снимките на Фигура 1 няма значение къде започва отклонението. Но не винаги е така:
Задача 2 Проследете (всички редове веднъж!) картина от серията на фиг. 2.
По тези пътеки планинаспасителят вече не може да се върне на същото място, като обиколи всички следи веднъж. Необходимо е да се реши къде да се построят две колиби, за да може всеки ден да ходи от едната до другата и последователно да нощува в едната, а след това в тази. (И, разбира се, трябва да начертаете план за обход.)
В първите снимки на фиг. 2 отговорът е очевиден, последният не е. Ако това работи, можем допълнително да усложним въпроса:
Задача 3 Коя от картинките на фиг. 3 могат да бъдат оградени с една линия, без да се вдига моливът от хартията, и кои не могат да бъдат нарисувани, независимо къде започва заобикалянето?
Снимки като тези на фиг. 2 и 3 може да се нуждаят от много. Не е нужно да са смислени или симетрични; можете например да начертаете няколко точки по краищата на картината и да ги свържете с линии по произволен начин (фиг. 4).
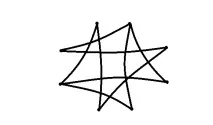
Задача 4 Коя линия (или линии) трябва да се добави в снимките на фиг. 3 за да направите байпаса възможен?
Проблем 5 И какво трябва да се добави, за да стане възможно заобикалянето от всяка точка?
Друг въпрос за сигурността:
Задача 6 Нарисувайте две картини, които могат да бъдат оградени, но трябва да изберете правилната начална точка, и две, които не могат да бъдат оградени.
Тази задача, разбира се, ще има особен успех и особено нетривиални решения, ако бъде представена като тест за един от възрастните.
И накрая, последната задача, с решението на която "очертанията" могат да се считат за преминат етап: