Матрични модели
Учебници за ВУЗ
Екология и безопасност на живота
9.4. Матрични модели
Матричният модел може да се разглежда като аналог на динамичния модел с крайна разлика. Ранна версия на матричния модел е разработена от Люис и Лесли [30] като детерминистичен модел, който прогнозира бъдещата възрастова структура на женското население от известна структура към настоящия момент и хипотетични коефициенти на оцеляване и раждаемост. Популацията е разделена наn+1 възрастови групи (т.е. 0, 1, 2.n,като всяка група се състои от индивиди на една и съща възраст), така че най-старата група или групата, в която всички животни, оцелели до дадена възраст, измират, има номерn.Означавайки сxnброя на индивидите във всяка възрастова група, получаваме вектор, представящ възрастовата структура в моментt.
Моделът се описва с матричното уравнение
(9.19)
което пишем в разширена форма:
където стойноститеfi ,(i =0,1.n) представляват броя на женските, произведени от женскатаi-та възраст,
р, (i =0.1.п -1) – вероятността женскатаi-та възраст да доживее до възрастi+1.
Нека покажем, че поведението на модела може да бъде предсказано чрез анализиране на някои формални свойства на матрицатаA.Първо, чрез последователно умножаване на уравнението (9.19) по матрицатаA,, е лесно да се получат по-общи уравнения за броя на възрастовите групи по време на
(9.21)
Второ, тъй като матрицатаAе квадратна с (n+1) редове и колони, тя имаn+1 собствени стойности (отчитане на множествеността) и (n+1) собствени (и свързани) вектори. ЕлементиAса или положителни числа, или нула, така че най-голямата (по абсолютна стойност) собствена стойност и координатите на съответния собствен вектор са положителни и в същото време имат определено екологично значение. Нека илюстрираме това с един от най-простите модели, предложен от Уилямсън [54].
Първоначалната популация има вектор, представящ възрастовата структураa0 =(0,0,1), т.е. популацията се състои от една по-възрастна женска. МатрицатаAима формата:
След един интервал от време имаме
т.е.a1 = (12, 0, 0) и вече ще има 12 по-млади женски в популацията. Повторното прилагане на модела дава следните резултати:
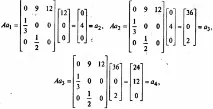
Основната собствена стойност и собственият вектор на матрицатаAмогат да бъдат намерени по известни методи, като
(9.22)
или задаване на–система от линейни алгебрични уравнения
Следователно основната собствена стойност λ1=2 и собственият вектор, дължащ се на (9.23), имат формата = (24, 4,1). Останалите собствени стойности, по силата на (9.24), имат формата λ2=-1,λ3=-1. Поради (9.23), собственият вектор има формата = (6,-2,1). Тъй като собствената стойност -1 е двойна, тогава, за да намерим вектора (наречен асоцииран), решаваме системата от уравнения(A - λ2) = :