Механично значение на втората производна

Нека материалната точка се движи праволинейно по закона s=s(t), където s е пътят, изминат от точката за време t. Тогава скоростта v на това движение е v= s'(t) = v(t), т.е. също е някаква функция на времето.

В момент t скоростта има стойност v=v(t). Нека разгледаме друг момент от време t+Δt. Тя съответства на стойността на скоростта v1 = v(t+Δt). Следователно нарастването на времето Δt съответства на увеличението на скоростта Δv= v1 – v = v(t + Δt) – v(t). Поведение

се нарича средното ускорение за интервала от време Δt.

Ускорението в даден момент t е границата на средното ускорение при Δt→0:

По този начин ускорението на праволинейното движение на точка е производната на скоростта по отношение на времето. Но както вече видяхме, скоростта е производната на пътя s по отношение на времето t: v = s'. Имайки предвид това, имаме:

тези. ускорението на праволинейното движение на точка е равно на 2-ра производна на пътя по време

43. Диференциали. Геометричният смисъл на диференциала. диференциални свойства.

Диференциали

За функции

Диференциалът на функция в точка може да се дефинира като линейна функция

където означава производната в точката .

Така има функция от два аргумента.

Диференциалът може да се дефинира директно, т.е. без да се включва дефиницията на производната, като функция, която зависи линейно от и за която е вярна следната връзка

За дисплеи

Диференциалът на картографиране в точка е линеен оператор, така че условието

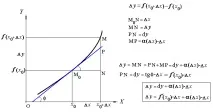
Геометричното значение на диференциала

Диференциалът на функцията f(x) в точката x0 е равен на увеличението, което ординатата на допирателната към кривата y=f(x) с абсцисата в точката x0 получава при преместване от точката на контакт към точката с абсцисата x0+Δx.

Диференциални свойства

Диференциалът на функцията има свойства, подобни на тези на производната.

1.Диференциалът на константата е равен на нула: dc = 0, с = const.

2.Диференциалът на сбора от диференцируеми функции е равен на сбора от диференциалите на членовете:

Последица. Ако две диференцируеми функции се различават с постоянен член, тогава техните диференциали са

d(u+c) = du (c= const).

3.Диференциалът на произведението на две диференцируеми функции е равен на произведението на първата функция по диференциала на втората плюс произведението на втората по диференциала на първата:

Последица. Постоянният фактор може да бъде изваден от знака на диференциала

d(cu) = cdu (c = const).

4.Диференциалът u/v на две диференцируеми функции u = u(x) и v = v(x) се определя от формулата

5. Свойството за независимост на формата на диференциала от избора на независима променлива (инвариантност на формата на диференциала): диференциалът на функция е равен на произведението на производната и диференциала на аргумента, независимо дали този аргумент е независима променлива или функция на друга независима променлива.

44. Основни теореми на диференциалното смятане (теорема на Ферма, теорема на Рол, теорема на Лагранж).

Теорема на Ферма

Теоремата гласи, че:

За всяко естествено число уравнението няма естествени решения , и .

Теорема на Рол

(Теорема на Рол ) Нека функциятаf(x)

непрекъснат в интервала [a,b];
диференцируеми в интервала (a,b);
в краищата на сегмента [a,b] приема равни стойности.

Тогава има смисълcO (a,b), така чеf'(c) = 0.

Доказателствое дадено в I.M. Петрушко и Л.А. Кузнецова „Курс по висша математика: Въведение в математическия анализ. Диференциално смятане." М .: Издателство МЕИ, 2000. Стр. 118.

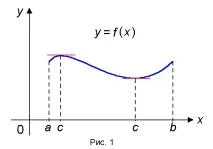
Геометрична интерпретация на теоремата на Рол

От теоремата на Рол следва, че има точка с O (a,b), в която допирателната към графиката на функциятаf(x) е успоредна на оста OX(фиг. 1).

Теорема на Лагранж

(Теорема на Лагранж ) Нека функциятаf(x)

Тогава има точка с O (a,b), така че

f(b) −f(a) =f'(c) (b−a) .

(1)

Формула (1) се наричаформула на Лагранж илиформула за ограничено нарастване