Методи за програмиране

Задача 4. Топологично сортиране на върховете на графа

Главна информация

Задачата се състои от две части, първата от които е задължителна, втората се изпълнява за получаване на оценка „отличен“.

Двоично отношениевърху множество A е подмножество на декартовото произведение M x M, т.е. някакво множество от подредени двойки, всеки елемент от които е елемент от множеството A . Например релацията > (по-голямо от) е двоична релация в множеството и съдържа двойки (2, 1), (3, 1), (4, 1), (3, 2), (4, 2), (4, 3) . Ще кажем, че твърдението a R b е вярно, ако двойката (a, b) принадлежи на двоичното отношение R .

Нека някакво бинарно отношение R е дадено върху крайно множество A . Задачата на топологичното сортиране е да подреди елементите на множеството A в последователността a1, a2, . aN, така че за всяка двойка (ai, aj), така че ai R aj е вярно, условието i е изпълнено.

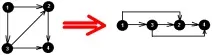
Ако представим връзката като насочен граф (елементите на множеството са върхове, ръбът от връх a до връх b съществува тогава и само ако a R b е вярно), тогава проблемът може да се формулира по следния начин: избройте върховете на графа в такъв ред, че за всяко ребро на графа началният му връх да е посочен преди последния. Фигурата отляво показва оригиналния граф, отдясно неговите върхове са изброени в необходимия ред.

Ето пример за използване на топологично сортиране: да предположим, че има редица задачи, някои от които не могат да бъдат изпълнени, докато не бъдат изпълнени някои други задачи. Този набор от задачи е представен като насочен граф и в резултат на топологично сортиране на върховете на този граф,последователност от задачи, която отговаря на всички условия.

Ясно е, че е възможно да се извърши топологично сортиране не във всеки граф, а само в такъв, в който няма цикли. Алгоритъмът, описан по-долу, извършва топологично сортиране на граф без цикли.

Маркираме всички върхове на графа като неизползвани.
Търсим неизползван връх, който не включва никакви ребра (има само нули в съответната колона на матрицата на съседство). Ако няма такъв връх, тогава или сме преминали през всички върхове (топологичното сортиране е приключило), или има цикъл в графа (топологичното сортиране е невъзможно).
Маркираме намерения връх като използван, отпечатваме неговия номер.
Премахваме от графиката всички ръбове с начало в този връх (съответният ред на матрицата на съседство е настроен на нула).
Да преминем към стъпка 2.

За да ускорите алгоритъма, можете да съхраните в масива броя на ръбовете, включени в даден връх, и да актуализирате този номер, когато изтривате всеки ръб.

Формулиране на задача

а. Внедряване върху матрици на съседство.

Входният файл input.txt съдържа графика като списък от ребра. Прочетете го в матрица на съседство (двумерен масив, чийто елемент (i, j) е равен на 1, ако графиката има ребро от връх i до връх j, и 0 в противен случай) и извършете топологично сортиране на тази графика. Изведете резултата (последователност от върхове или съобщение за наличието на цикъл в графиката) във файла output.txt.

b. *Внедряване на списъци за съседство.

Същата задача, но съхранявайте графиката като списък на съседство (за всеки връх се съхранява списък от върхове, който има ребро от този връх).