MI 2083-90 GSI
ДЪРЖАВНО ЕДИНСТВО НА СИСТЕМАТА ЗА ИЗМЕРВАНЕ
ОПРЕДЕЛЯНЕ НА РЕЗУЛТАТИТЕ ОТ ИЗМЕРВАНЕТО И ОЦЕНКА НА ТЯХНАТА ГРЕШНОСТ
КОМИТЕТ ПО СТАНДАРТИЗАЦИЯ И МЕТРОЛОГИЯ НА СССР
1. ОБЩИ ПОЛОЖЕНИЯ
2. КОСВЕНИ ИЗМЕРВАНИЯ С ЛИНЕЙНА ЗАВИСИМОСТ
3. КОСВЕНИ ИЗМЕРВАНИЯ С НЕЛИНЕЙНА ЗАВИСИМОСТ
4. МЕТОД НА РЕДУКЦИЯ
5. ФОРМИ НА ПРЕДСТАВЯНЕ НА РЕЗУЛТАТА ОТ ИЗМЕРВАНЕТО
ТЕРМИНИ И ОПРЕДЕЛЕНИЯ, ИЗПОЛЗВАНИ В ПРЕПОРЪКАТА
КРИТЕРИИ ЗА ОТСУТСТВИЕ НА КОРЕЛАЦИЯ МЕЖДУ ГРЕШКИТЕ НА РЕЗУЛТАТИТЕ ОТ ИЗМЕРВАНЕТО НА АРГУМЕНТИТЕ
GSI. ИЗМЕРВАНИЯ ИНДИРЕКТНИ
Определяне на резултатите от измерването и оценка на техните грешки
Дата на въвеждане01.01.92
Тази препоръка се прилага за регулаторна и техническа документация, съдържаща методи за извършване на непреки измервания, и установява основните разпоредби за определяне на резултатите от измерването и оценка на техните грешки, при условие че аргументите, от които зависи измерената стойност, се приемат като постоянни физически величини; известните систематични грешки в резултатите от измерването на аргументите се изключват, а неизключените систематични грешки се разпределят равномерно в дадените граници ± θ.
Термините и определенията, използвани в тази препоръка, са дадени в Приложение 1.
1. ОБЩИ ПОЛОЖЕНИЯ
1.1. Желаната стойност на физическата величинаAсе намира въз основа на резултатите от измерването на аргументитеа1, . . . ,и i, . . . ,а m, свързани с желаната стойност чрез уравнението
. (1)
Функциятаfтрябва да бъде известна от теоретичната основа илиустановено експериментално с грешка, която може да бъде пренебрегната.
1.2. Резултатите от измерванията на аргументите и оценката на техните грешки могат да бъдат получени от преки, непреки, кумулативни, съвместни измервания. Информация за аргументите може да бъде взета от справочна литература, техническа документация.
1.3. Когато се оценяват доверителните граници на грешките в резултата от непряко измерване, обикновено се приема вероятност, равна на 0,95 или 0,99. Използването на други вероятности трябва да бъде обосновано.
1.4. Основните разпоредби на препоръката са установени за оценка на индиректно измереното количество и грешките на резултата от измерването:
с линейна зависимост и липса на корелация между грешките на измерване на аргументите (раздел 2);
с нелинейна зависимост и без корелация между грешките на измерване на аргументите (раздел 3);
за корелирани грешки на измерване на аргументи при наличие на серия от индивидуални стойности на измерените аргументи (раздел 4).
Забележка. Критерият за проверка на хипотезата за липсата на корелация между грешките на измерване на аргументите е даден в Приложение 2.
2. КОСВЕНИ ИЗМЕРВАНИЯ С ЛИНЕЙНА ЗАВИСИМОСТ
2.1. Стойността за търсенеAе свързана сmизмерените аргументиa1,a2, . . . ,amпо уравнението
Няма корелация между грешките на измерване на аргументите.
Забележка. Ако коефициентитеb1 ,b2 .bmсе определя експериментално, след което задачата за определяне на резултата от измерването на стойността се решава на етапи: първо се оценява всеки членbi·ai; като индиректно измерена стойност, получена в резултат на произведението на две измерени стойности, и след това намерете оценката на измерената стойностA.
2.2.Резултатът от косвеното измерване се изчислява по формулата
(3)
където е резултатът от измерването на аргументаи i;m- брой аргументи.
2.3. Стандартното отклонение на резултата от косвеното измерване се изчислява по формулата
(4)
където е стандартното отклонение на резултата от измерването на аргументаai.
2.4. Доверителните граници на случайната грешка на резултата от косвеното измерване, при условие че разпределението на грешките в резултатите от измерванията на аргументите не противоречи на нормалните разпределения, се изчислява (без да се взема предвид знакът) по формулата
(5)
къдетоtq, - Коефициентът на Стюдънт, съответстващ на доверителната вероятностP= l -qи броя на степените на свободаfeff , изчислен по формулата
(6)
къдетоni, е броят на измеренията при дефиниране на аргументаai, .
2.5. Границите на неизключената систематична грешка на резултата от косвеното измерване се изчисляват, както следва.
2.5.1. Ако неизключените систематични грешки на резултатите от измерването на аргументите са дадени от границите θi; тогава доверителните граници на неизключената систематична грешка на резултата от косвеното измерване Θ(p) (без да се взема предвид знакът) с вероятностPсе изчисляват по формулата
(7)
къдетоkе корекционен фактор, определен от приетата доверителна вероятност и брояmна компонентите Θi.
При ниво на достоверностP= 0,95, корекционният факторkсе приема равен на 1,1.
С доверителна вероятностP= 0,99, корекционният фактор се приема равен на 1,4, ако броят на сумираните компоненти еm>4. Ако броят на компонентитеm≤4, тогава корекционният коефициентk≤1,4; по-точна стойностkможе да бъде намерена с помощта на диаграмата на зависимостта
къдетоmе броят на сумираните компоненти (аргументи);l- параметър в зависимост от съотношението на границите на компонентите.
На графиката крива1показва зависимостта наkотlприm= 2, крива2- приm= 3, крива3- приm= 4.
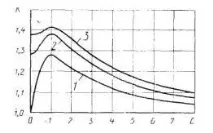
Грешката, която възниква при използване на формула (7) за сумиране на неизключени систематични грешки, не надвишава 5% (изчисленията са получени въз основа на анализа на резултатите от съставите на равномерни разпределения).
2.5.2. Ако границите на неизключените систематични грешки на резултатите от измерването на аргументите са дадени чрез доверителни граници, съответстващи на вероятноститеPi, (границите на неизключените систематични грешки на резултатите от измерването на аргументите се изчисляват по формулата (7), тогава се изчисляват границите на неизключената систематична грешка на резултата от непрякото измерване за вероятносттаP(пренебрегвайки знака) по формулата
(8)
За вероятностP= 0.95ki= 1.1; заP= 0,99, стойностите на коефициентитеkiсе определят в съответствие с точка 2.5.1.
2.6. Грешката на косвения резултат от измерването се оценява въз основа на състава на разпределенията на случайни и неизключени систематични грешки.
2.6.1. Ако , тогава неизключеният систематичен компонент на грешката на измерване се приема като грешка на косвения резултат от измерването и неговите граници се изчисляват в съответствие с точка 2.5.
2.6.2. Ако , грешката на резултата от непрякото измерване се приема като случаен компонент на грешката на измерване и нейните граници се изчисляват в съответствие с точка 2.4.
2.6.3. Ако , тогава доверителната граница на грешкатарезултатът от непрякото измерване ∆(P) се изчислява (без да се взема предвид знакът) по формулата
къдетоKе коефициент, зависещ от нивото на достоверност и от отношението.
Стойности на коефициентаKв зависимост от отношението за вероятностP= 0,95 иP= 0,99: