Модулация с минимално изместване на честотата - Комуникации и комуникации
3.3 Модулация с минимално изместване на честотата.
Една схема за непрекъсната модулация е манипулацията с минимално изместване на честотата (MSK). MSK може да се разглежда като специален случай на честотна манипулация без фазово прекъсване. MSK сигналът може да бъде представен по следния начин.
Тук f0 е носещата честота, dk=±1 представлява биполярни данни, които се предават при R=1/T, а xk е фазовата константа за k-тия битов интервал. Обърнете внимание, че когато dk=1 предаваната честота е f0+1/4T, а когато dk=-1 е f0-1/4T. По време на всеки T-секунден интервал на предаване на данни стойността на xk е постоянна, т.е. xk=0 или π, което е продиктувано от изискването за непрекъснатост на фазата на сигнала в моменти t=kT. Това изискване налага ограничение на фазата, което може да бъде представено чрез следната рекурсивна връзка за xk.
Уравнението за s(t) може да бъде пренаписано в квадратурно представяне.
Синфазният компонент се обозначава като akcos(πt/2T)cos2πf0t, където cos2πf0t е носителят, cos(πt/2T) е синусоидалното тегло на символа и ak е членът, зависим от данните. По подобен начин, квадратурният компонент е bksin(πt/2T)sin2πf0t, където sin2πf0t е носещият квадратурен член, sin(πt/2T) е същото синусоидално тегло на символа и bk е зависимият от информация член. Може да изглежда, че стойностите ak и bk могат да променят стойността си на всеки T секунди. Въпреки това, поради изискването за фазова непрекъснатост, стойността на ak може да се промени само когато функцията cos(πt/2T) премине през нула, а bk само когато sin(πt/2T) премине през нула. Следователно претеглянето на символа в синфазен или квадратурен канал е синусоидален импулс с период 2T и променлив знак. Синфазните и квадратурните компоненти са изместениедин спрямо друг за T секунди.
Изразът за s(t) може да бъде пренаписан в различна форма.
Тук dI(t) и dQ(t) имат едно и също значение на синфазни и квадратурни потоци от данни. MSK схема, написана в тази форма, понякога се нарича предварително кодиран MSK. Графичното представяне на s(t) е дадено на фиг. 3.4. На фиг. 3.4. a) и c) показва синусоидалното претегляне на синфазните и квадратурните канални импулси, тук умножението по синусоида дава по-плавни фазови преходи, отколкото в оригиналното представяне на данните. На фиг. 3.4. b) и d) показва модулацията на ортогоналните компоненти cos2πf0t и sin2πf0t чрез синусоидални потоци от данни. На фиг. 3.4. д) сумирането на ортогоналните компоненти, показани на фиг. 3.4. б) и г). От израза за s(t) и фиг.3.4. можем да заключим следното: 1) сигналът s(t) има постоянна обвивка; 2) RF носещата фаза е непрекъсната при битови преходи; 3) сигналът s(t) може да се разглежда като FSK модулиран сигнал с честоти на предаване f0+1/4T и f0-1/4T. По този начин минималното разстояние между тоновете, необходимо за MSK модулация, може да бъде записано като:
което е равно на половината от побитовата скорост. Имайте предвид, че разстоянието между тоновете, необходимо за MSK, е половината (1/T) от разстоянието, необходимо за некохерентно откриване на FSK модулирани сигнали. Това е така, защото носещата фаза е известна и непрекъсната, което позволява кохерентна демодулация на сигнала. [2]
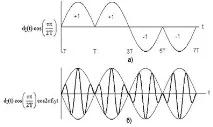
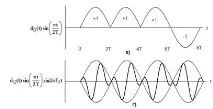
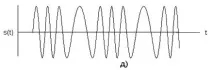
Ориз. 3.4. Минимална манипулация на изместване: а) модифициран синфазен битов поток; б) произведението на синфазния битов поток и носителя; c) модифициран квадратурен битов поток; d) произведението на квадратурния битов поток и носителя; д) MSK сигнал.
3.4 Квадратурна модулацияи неговите характеристики (QPSK, QAM)
Помислете за квадратурно фазово изместване (QPSK). Първоначалният поток от данни dk(t)=d0, d1, d2,… се състои от биполярни импулси, т.е. dk вземете стойностите +1 или -1 (фиг. 3.5.a)), представляващи двоична единица и двоична нула. Този импулсен поток е разделен на синфазен поток dI(t) и квадратурен - dQ(t), както е показано на фиг. 3.5.б).
Удобна ортогонална реализация на QPSK сигнала може да бъде получена с помощта на амплитудна модулация на синфазните и квадратурните потоци върху синусовите и косинусовите функции на носителя.
Използвайки тригонометрични идентичности, s(t) може да се представи по следния начин: s(t)=cos(2πf0t+θ(t)). QPSK модулаторът, показан на фиг. 3.5.c), използва сумата от синусоидалните и косинусовите членове. Импулсният поток dI(t) се използва за амплитудна модулация (с амплитуда +1 или -1) на косинусовата вълна. Това е еквивалентно на изместване на фазата на косинусовата вълна с 0 или π; следователно резултатът е BPSK сигнал. По подобен начин импулсният поток dQ(t) модулира синусоида, която дава BPSK сигнал, ортогонален на предишния. Когато тези две ортогонални носещи компоненти се сумират, се получава QPSK сигнал. Стойността на θ(t) ще съответства на една от четирите възможни комбинации на dI(t) и dQ(t) в израза за s(t): θ(t)=0 0 , ±90 0 или 180 0 ; получените сигнални вектори са показани в сигналното пространство на фиг. 3.6. Тъй като cos(2πf0t) и sin(2πf0t) са ортогонални, двата BPSK сигнала могат да бъдат открити отделно. QPSK има редица предимства пред BPSK: при QPSK модулация един импулс предава два бита, след което скоростта на данни се удвоява или при същата скорост на данни като в схемата BPSK се използва половината от честотната лента; както и повишена устойчивост на шум, т.к. пулс два пъти.по-дълги и следователно по-мощни от BPSK импулсите. [2]
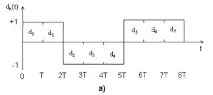
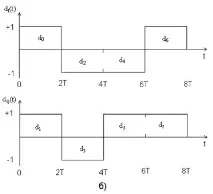
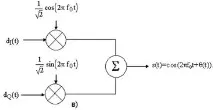
Ориз. 3.5. QPSK модулация.
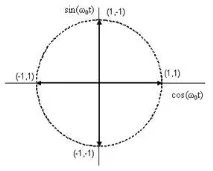
Ориз. 3.6. Сигнално пространство за схемата QPSK.
Квадратурната амплитудна модулация (KAM, QAM) може да се счита за логическо разширение на QPSK, тъй като QAM сигналът също се състои от две независими амплитудно модулирани носители.
При квадратурна амплитудна модулация както фазата, така и амплитудата на сигнала се променят, което позволява да се увеличи броят на кодираните битове и в същото време значително да се увеличи устойчивостта на шум. Квадратурното представяне на сигнали е удобно и доста универсално средство за тяхното описание. Квадратурното представяне се състои в изразяване на трептенето като линейна комбинация от две ортогонални компоненти - синусоидална и косинусова (синфазна и квадратурна):
s(t)=A(t)cos(ωt + φ(t))=x(t)sinωt + y(t)cosωt, където
Такава дискретна модулация (ключ) се извършва по два канала, на носители, изместени с 90 0 един спрямо друг, т.е. в квадратура (оттук и името).
Нека обясним работата на квадратурната верига, като използваме примера за формиране на четирифазни FM сигнали (FM-4) (фиг. 3.7).
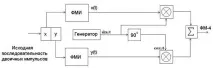
Ориз. 3.7. Схема на квадратурния модулатор.
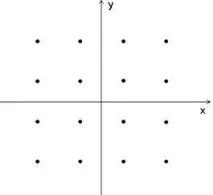
Ориз. 3.8. Шестнадесетично сигнално пространство (QAM-16).
Първоначалната последователност от двоични символи с продължителност T се разделя от регистър за изместване на нечетни импулси y, които се подават в квадратурния канал (cosωt), и четни импулси x, които влизат във фазовия канал (sinωt). И двете последователности от импулси се подават към входовете на съответните манипулирани формировачи на импулси, на изходите на които се формират последователности от биполярни импулси x(t) и y(t) самплитуда ±Um и продължителност 2T. На входовете на каналните умножители постъпват импулси x(t) и y(t), на изходите на които се формират двуфазни (0, π) ЧМ колебания. След сумирането те формират сигнала FM-4.
На фиг. 3.8. Показани са 2D сигнално пространство и набор от шестнадесетични QAM-модулирани сигнални вектори, изобразени от точки, подредени в правоъгълен масив.
От фиг. 3.8. може да се види, че разстоянието между сигналните вектори в сигналното пространство с QAM е по-голямо, отколкото с QPSK, следователно QAM е по-устойчив на шум в сравнение с QPSK,