Мономолекулно адсорбционно уравнение на Langmuir
Експериментално са получени адсорбционните изотерми на различни ПАВ. Всички те са с еднаква форма – има хоризонтално сечение (фиг. 11). За вещества от една и съща хомоложна серия всички изотерми се сливат в границата (фиг. 12.). Това може да бъде при условие, че: 1) всички молекули от хомоложната серия, независимо от дължината на въглеводородната верига, заемат една и съща област на интерфейса; 2) адсорбционният слой е с дебелина не повече от една молекула, т.е. мономолекулен.
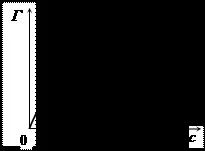
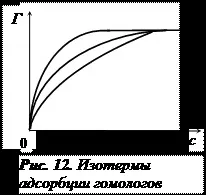
Уравнението на Гибс не описва цялата експериментално получена изотерма на адсорбция. Спомнете си, че работи само при ниски концентрации на повърхностно активно вещество. Изотермите на мономолекулярната адсорбция са добре описани от уравнението на Langmuir.
Уравнението на Langmuir е получено за адсорбция на газ върху твърда повърхност, но е приложимо и за описване на адсорбция при повърхностно активно вещество-разтвор на повърхността. Освен това, именно за интерфейса твърдо вещество-газ, за който е получен, по-често се наблюдават различни видове отклонения от адсорбционната изотерма на Langmuir.
Основните положения на теорията на Langmuir ще бъдат дадени при разглеждане на адсорбцията върху твърда повърхност. В тази глава се ограничаваме до извеждането на уравнението.
Помислете за интерфейса течност-газ с площ от 1 m 2.
НекаQе повърхностната площ, заета от молекулите на повърхностно активното вещество;
(1-Q) – свободна площ;
na е броят на частиците (молекулите), адсорбирани за единица време;
nd е броят на десорбираните частици.
При равновесие скоростта на адсорбция е равна на скоростта на десорбция, т.е.
Скоростта на адсорбция е пропорционална на частта от свободната площ на повърхностния слой и концентрацията на повърхностно активното вещество в разтвора
скоростта на десорбция зависи само от частта от запълнената повърхностповърхностноактивни молекули:
Решете заQ:
.
Разделете числителя и знаменателя наkd:
,
kа/ke =k– адсорбционно-десорбционна равновесна константа,
. (10)
Площта на повърхностния слой, изпълнен с молекули на повърхностно активното вещество, може да се намери като произведение на площта, заета от една молекула на повърхностно активното веществоS0 от броя на молекулите в повърхностния слойN = nNa, къдетоnе количеството вещество в повърхностния слой,Naе числото на Авогадро,Na= 6,02×10 2 3 mol -1.
Количеството вещество на единица площ от повърхностния слой е адсорбциятаГна даденото вещество. Тъй като извеждането на уравнението разглежда повърхностен слой с площ от 1 m 2,n=Г. Когато повърхностният слой е наситен с молекули на ПАВQ =1 m 2n=Gмакс.
.
Заместете в уравнение (10):
. (единадесет)
Уравнение (11) е уравнението на Langmuir, описващо мономолекулната адсорбционна изотерма.
При много ниски концентрации на повърхностно активно веществоkc>gt; 1 иГ=Гmax е хоризонталната част на адсорбционната изотерма.
По този начин, за разлика от уравнението на Гибс, уравнението на Langmuir описва цялата изотерма на адсорбция.
За намиране на константите на уравнението на ЛангмюрГmax иkто се привежда в линеен вид. След линеаризация
къдетоy= 1/Г,х= 1/С, 1/Гmax =a(свободен член), 1/k Гmax =b(наклон)
Постройте графика в координатите 1/G= f(1/s) (фиг. 13). Съгласно графиката се определят свободният член a и наклонът b (тангенса на наклона tg a), според които се намират стойноститеГmax иk.
Познавайки граничната адсорбцияГmax, е възможно да се изчисли дължината на молекулатаПовърхностноактивно веществоlи площта, заета от една молекула в повърхностния слойS0.
На повърхността на фазовия интерфейс от 1 m 2 еGmaxNамолекули на повърхностно активното вещество.
В състояние на най-плътна опаковка, съответстващо на наситен повърхностен слой, тези частици заемат площГmaxNаS0 = 1.
Обемът на наситения повърхностен слой, съответстващ на площ от 1 m 2, е, от една страна,Gmax×M/r и 1×l –от друга. Последното твърдение е правилно, ако приемем, че дебелината на повърхностната зона е равна на дължината на молекулатаl. В този случай равенството
,
къдетоMе моларната маса на повърхностно активното вещество;rе плътността на повърхностно активното вещество.
При ниски концентрации на повърхностноактивни вещества изчисляването на адсорбцията с помощта на уравненията на Гибс и Лангмюр дава подобни резултати, т.е. десните страни на тези уравнения могат да бъдат приравнени:
,
.
Интегрирайки в определени граници от 0 доsи отs0 доs, получаваме:
.
Сравнявайки полученото уравнение с уравнението на Шишковски (1), е лесно да се установи връзка между константите на двете уравнения:
и константатаkв уравненията на Шишковски и Лангмюр е константата на адсорбционно-десорбционното равновесие.