Мрежи на Петри - Създаване на програма за управление на гъвкава производствена система
Предназначение на мрежите на Петри
Мрежите на Петри са инструмент за графично и математическо моделиране, приложим към системи от различни видове. Системите могат да съдържат голям брой взаимодействащи си елементи, всеки елемент от своя страна също може да бъде система с много компоненти, които взаимодействат един с друг по сложни начини. Примери за такива системи са икономически системи, правни, химически, биологични системи и системи за управление.
Те представляват обещаващ инструмент за описание и изследване на мултипрограмни, асинхронни, разпределени, паралелни, недетерминирани и/или стохастични системи за обработка на информация. Като графичен инструмент, мрежите на Петри могат да се използват за визуално представяне на системата, която се моделира, подобно на блок диаграми, блок диаграми и мрежови диаграми. Концепцията за чипове, въведена в тези мрежи, позволява да се моделира динамиката на функционирането на системите и паралелните процеси. Като математически инструмент, аналитичното представяне на мрежата на Петри позволява да се съставят уравнения на състоянието, алгебрични уравнения и други математически зависимости, които описват динамиката на системите. В момента мрежите на Петри се използват главно в моделирането. В много области на изследване феноменът се изучава не директно, а индиректно, чрез модел. Моделът е представяне, обикновено в математически термини, на това, което се счита за най-характерно за обекта или системата, които се изучават. Чрез манипулиране на модела на системата, човек може да получи нови знания за него, избягвайки опасността, високата цена или неудобството от анализирането на самата реална система. Обикновено моделите имат математическа основа.
Развитието на теорията на мрежите на Петри се извършва в две посоки.Формалната теория на мрежите на Петри се занимава с разработването на основните инструменти, методи и концепции, необходими за прилагането на мрежите на Петри. Приложната теория на мрежите на Петри се занимава главно с приложението на мрежите на Петри за моделиране на системи, техния анализ и произтичащото от това дълбоко проникване в моделираните системи.
Моделирането в мрежите на Петри се извършва на ниво събитие. Той определя какви действия се извършват в системата, какви състояния са предшествали тези действия и какви състояния ще приеме системата след извършване на действието. Изпълнението на модела на събитията в мрежите на Петри описва поведението на системата. Анализът на резултатите от изпълнението може да разкаже за състоянията, в които системата е била или не, кои състояния по принцип не са постижими. Такъв анализ обаче не дава числени характеристики, които определят състоянието на системата. Въпреки предимствата на мрежите на Петри, описани по-горе, неудобството от използването на мрежите на Петри като език за програмиране се крие в процеса на тяхното изпълнение в компютърна система. В мрежите на Петри няма строга концепция за процес, който може да бъде изпълнен на определен процесор. Също така няма недвусмислена последователност на изпълнение на мрежата на Петри, тъй като оригиналната теория ни предоставя език за описание на паралелни процеси. Мрежите на Петри са един от най-разпространените съвременни формализми за моделиране и анализ на паралелни разпределени системи. В момента се провеждат голям брой теоретични и практически изследвания за разработване на разпределени алгоритми, базирани на мрежи на Петри. В същото време експертите изпитват необходимост от развитие на формализъм, за да представят по-адекватно и удобно системи със сложна структура. Провеждат се изследвания за разширяване на мрежите на Петри сдобавяне на проекти, които отразяват модулността и йерархията на системите, както и подпомагане на развитието стъпка по стъпка чрез последователно детайлизиране.
Дефиниция на мрежа на Петри
Мрежата на Петри (Фигура 3) се дефинира като двустранен насочен граф, всички върхове на графа принадлежат към един от двата класа:
Позициите са представени с кръгове, преходите с линейни сегменти. Дъгите в мрежите на Петри са насочени.
Мрежата на Петри се състои от 4 елемента:
P = - Набор от позиции.
T = - Набор от преходи.
Функция за въвеждане "I": показване на входни позиции за преходи.
Изходна функция "O": показва изходните позиции за преходи.
Елементарната мрежа на Петри е показана на фиг. 3.
рисуване. 3. Елементарна мрежа.
Етикетиране на мрежи на Петри
Етикетирането се използва за моделиране на динамичните свойства на системата.
Маркировката M е разпределението на чипове към позициите на мрежата. Чипът е основна концепция на мрежите на Петри (като позиции и преходи). Чиповете са присвоени на позиции, но техният брой и позиция могат да се променят по време на изпълнението на мрежата на Петри.
На графиката на мрежата на Петри чиповете обикновено се изобразяват като малка точка в позиционен кръг. Ето пример за графично представяне на означена мрежа на Петри:
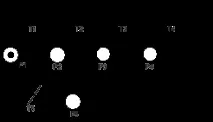
Фигура 4. Етикетиране на мрежи на Петри.
Маркирането (етикетът) на мрежата на Петри е функция, която преобразува набор от позиции в набор от неотрицателни цели числа.
Маркирането може да се дефинира като -вектор: , където и всеки () е . Векторът определя за всяка позиция на мрежата на Петри броя точки (маркери, чипове) в тази позиция.
Белязана мрежа на Петри се нарича белязана. Маркираната мрежа на Петри е комбинация от мрежа на Петри и етикетиране: . Маркировка замрежи , , , .
Маркирането характеризира динамиката на промените в състоянията на системата, а динамиката на промените в състоянията се моделира чрез движението на точки по позициите на мрежата. Етикетирането може да се промени в резултат на задействане на преходи. Преход на маркирана мрежа с етикет се нарича разрешен, ако , т.е. всяка входна позиция съдържа поне толкова точки, колкото има дъги от тази позиция в . Всеки разрешен преход може да започне. В резултат на стартиране на прехода етикетирането на мрежата се променя на ново: от всяка входна позиция на прехода се премахват толкова точки, колкото дъги, водещи от до , и толкова точки се поставят във всяка изходна позиция, колкото дъги, водещи от до . Последователността от стартирания на прехода се нарича мрежово изпълнение.
Нека позициите и съдържат по една точка. Помислете за изпълнението на такава маркирана мрежа. В тази маркировка е разрешен само преходът. Когато се стартира, точката ще бъде премахната от , а след това в позиции и ще се появи точка по точка, тоест в резултат на стартирането ще се появи точка и в .
Сега преходите и са активирани. Тъй като всеки разрешен преход може да се задейства, приемете, че преходът е задействан. След стартирането му точката ще бъде премахната от позицията и в позицията ще се появи една точка. Не е разрешен преход в получената маркировка. Това приключва изпълнението на мрежата на Петри.
Казва се, че етикетът е директно достъпен от, ако има разрешен преход, така че когато започне, се получава етикет, т.е.
Казва се, че един етикет е достъпен от етикет, ако има последователност от преходи, чието задействане отвежда мрежата от етикет към етикет, т.е.
Множеството от достижими маркировки от мрежата на Петри се нарича множество от достижимост и се означава с .
Интерпретацията на мрежите на Петри се основава на понятията за условия и събития. Състоянието на системата се описва от набор от условия. Функционирането на системата е изпълнение на последователност от събития. За да се случи дадено събитие, трябва да бъдат изпълнени определени условия, наречени предпоставки.[4]
Настъпването на дадено събитие може да доведе до нарушаване на предпоставките и до появата на някои нови условия, наречени постусловия. В мрежата на Петри условията се моделират чрез позиции, събитията се моделират чрез преходи. Предварителните условия на дадено събитие са представени от входните позиции на съответния преход, постусловията са представени от изходните позиции. Появата на събитие се моделира чрез задействане на преход. Изпълнението на условията се изразява в наличието на точки в съответните позиции, неизпълнението - в липсата им.
Правила за създаване на мрежи на Петри
Мрежата на Петри се изпълнява чрез задействане на преходи. Задействането на прехода се контролира от токените в неговите входни позиции и е придружено от премахване на токени от тези позиции и добавяне на нови токени към неговите изходни позиции.
Преходът може да се изпълнява само ако е активиран. Преходът се нарича разрешен, ако всяка от неговите входни позиции съдържа броя на токените не по-малък от броя на дъгите, водещи от тази позиция към прехода (или кратността на входната дъга).
Изстрелванията могат да се извършват, стига да има поне един разрешен преход. Когато не останат разрешени преходи, изпълнението спира.
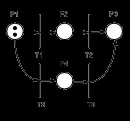
Фигура 5. Изпълнение на мрежа на Петри.
Свойства на мрежите на Петри
Безопасност. Позицията на мрежата на Петри с първоначална маркировка е безопасна, ако има такава. С други думи, позицията на мрежата на Петри е безопасна, ако броят на точките в нея никога не надвишава 1. Мрежата на Петри е безопасна, ако всичкипозиции в мрежата.
Ограничение. Разширение на защитното свойство. Сигурността е незадължително изискване. Позиция на мрежата на Петри с начален етикет е -ограничена или -безопасна, ако за всички , т.е. позиция е -ограничена, ако броят на точките в нея не надвишава цяло число . 1-безопасна позиция - просто безопасна позиция.
Мрежата, разбира се, може да съдържа позиции, чиято сигурност е различна. Въпреки това, ако една позиция е -безопасна, тогава тя също е -безопасна за всички. Следователно мрежата на Петри е -безопасна, ако всяка нейна позиция е -безопасна, къде е горната граница на сигурност на нейните позиции.
Често е важно да знаете дали броят на точките в дадена позиция е ограничен или не, а не конкретната стойност на границата. Една позиция се нарича ограничена, ако броят на точките в нея е краен. Мрежата на Петри е ограничена, ако всички нейни позиции са ограничени. Ограничена мрежа може да бъде внедрена хардуерно, мрежа с неограничени позиции обикновено не може да бъде внедрена хардуерно.
Запазване. Маркирането на позициите на мрежата на Петри може да моделира някои обекти или ресурси. За такива мрежи важно свойство е постоянството. Необходимо е точките, представляващи ресурси, да не изчезват или да се създават, когато се задействат преходи, тоест общият брой точки в мрежата трябва да остане постоянен.
Мрежа на Петри с първоначално етикетиране се казва, че строго запазва if
където е броят на позициите в мрежата.
Жизненост. Мрежата на Петри се нарича "жива" за дадено първоначално етикетиране, ако:
1. За всяка двойка маркировки (), принадлежащи към множеството, има място, т.е. има последователност от преходи, чиято работа прехвърля мрежата от маркировка към маркировка.
2. За всеки преход в комплекта има такава двойка маркировки (), че , тогаваима преходно изпичане, което извежда мрежата от маркировка към маркировка.
Активните и защитени мрежи се наричат правилни мрежи.
Дейност. Задънените улици са обект на много изследвания в системното моделиране. Задънена улица в мрежа на Петри е преход или набор от преходи, които не могат да бъдат задействани в някои маркировки и последващи маркировки. Преходът се нарича активен, ако не е блокиран (не е блокиран). Това не означава, че е позволено, по-скоро може да е позволено.
Има понятия, свързани с дейността, като нива на активност. Те могат да бъдат дефинирани за обозначена мрежа, както следва:
Ниво 0: Преходът има активност от ниво 0, ако никога не може да бъде задействан. Преход, който има активност от ниво 0, се нарича пасивен.
Ниво 1: Преходът има дейност от ниво 1, ако е потенциално задействан, т.е. ако съществува такъв, който е разрешен в .
Ниво 2: Преходът има активност от ниво 2, ако има последователност от изпълнение, в която се появява поне веднъж.
Ниво 3: Преходът има активност от ниво 3, ако има безкрайна последователност на изстрелване, в която той присъства неограничено често.
Ниво 4: Преходът има активност от ниво 4, ако е разрешен в която и да е маркировка.
Мрежата на Петри има ниво на активност, ако всеки от нейните преходи има ниво на активност не по-ниско от .