Неравномерност на разпределението
Както вече беше отбелязано в § 5.3, ако по-голямата част от съвкупността е разположена вляво от разпределителния център, има лявостранна асиметрия (0, тогава се наблюдава дясностранна асиметрия (дясно изкривяване). В същото време, за дясностранна асиметрия, неравенството> Me > Mo,се разклонява надясно);
§ = 0 - симетрично разпределение, тъй като опциите са на еднакво разстояние и имат еднаква честота, следователно = 0.
Оценката на степента на значимост на асиметрията се дава с помощта на средната квадратична грешка, която зависи от обема на наблюдениятаnи се изчислява по формулата:
=
Ако тогава асиметрията е значителна и разпределението на признака в съвкупността не е симетрично.
Ако тогава асиметрията е незначителна, нейното наличие се обяснява с влиянието на случайни фактори.
Куртоза на разпределението
За симетрични разпределения се изчислява показателятексцес (заостреност). Терминът "ексцекс" идва от латински. "excssus" - отстъпление, излишък.
Куртозата е разпределение с връх или плосък връх в сравнение със симетрично разпределение със същата сила на вариация.
С други думи, ексцесът е отклонението на върха на емпиричното разпределение надолу или нагоре от върха на кривата на симетрично (нормално) разпределение. В този случай ексцесът се определя само за симетрични и умерено асиметрични разпределения.
Индикаторът за ексцес се основава на използването на централен момент от четвърти ред и се изчислява по формулата:
където е централният момент от четвърти ред.
знак за коефициентопределя вида на разпределението:
§ if - разпределение с плосък връх;
§ if - симетрично разпределение;
§ if - пиково разпределение.
На фиг. 6.4 показва различни видове разпределения в зависимост от стойностите на индикатора за ексцес.
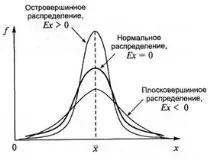
Фиг. 6.4. Ексцес на разпределение
Например, с отрицателен ексцес, разпределението е с плосък връх в сравнение с нормално разпределение. Ограничителната стойност на отрицателния ексцес е стойността .
При положителен ексцес разпределението е по-пиково от нормалното. Размерът на положителния ексцес е безкраен.
При симетрично (нормално) разпределение
Средната квадратична грешка на ексцеса зависи от броя на наблюденията n и се изчислява по формулата:
Ако съотношението приеме стойност, тогава отклонението от симетричното разпределение се счита за значително. Това показва съществения характер на ексцеса.
Оценката на значимостта на показателите за асиметрия и ексцес ни позволява да заключим дали това емпирично разпределение може да се припише на типа нормално разпределение.
Тестови въпроси
1. Какво се разбира под вариация на признак и какво е причинило необходимостта от изучаването му?
2. Назовете абсолютните и относителните показатели на вариация, дайте техните характеристики.
3. Избройте свойствата на дисперсията.
4. Формулирайте "правилото на трите сигми".
5. В какъв случай наборът от единици се счита за разнороден?
6. Как се определят средната стойност и дисперсията на алтернативен атрибут?
7. Какво е правилото за добавяне на отклонения?
8. За каква цел се използват различните видове дисперсии?
9. Как се оценява стегнатосттавръзки между черти?
10. Какви показатели на структурата на разпределението познавате?
11. Какви показатели за формата на разпределение познавате?
12. Дефинирайте понятието разпределителни моменти. Какви точки на разпространение познавате?
13. Какъв е методът на моментите?
14. Разкажете ни за асиметрията на разпределението и методите за нейното оценяване.
15. Какво се нарича ексцес на разпределението?
16. Каква е целта на оценката на значимостта на показателите за асиметрия и ексцес?