Номер на билет 19-2
ТОПЛИНЕН КАПАЦИТЕТ ПРИ НИСКИ ТЕМПЕРАТУРИ
За да проведем по-общо обсъждане на топлинния капацитет, първо отбелязваме, че в границата на голям кристал наборът от дискретни вектори, върху които се извършва сумиране в израза (23.12), става плътен в мащаба на онези характерни разстояния в k-пространството, при които членовете в (23.12) претърпяват значителни промени. Следователно можем да заменим сумата с интеграл, действайки съгласно общото правило (2.29) за произволен набор от вълнови вектори, които удовлетворяват граничните условия на Борн-Карман, и да напишем израз (23.12) като
където интеграцията трябва да бъде над първата зона на Брилюен. Като се вземат предвид опростяванията при много ниски температури, изразът (23.15) приема формата
където интегралът се взема върху цялото k-пространство.
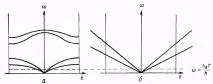
Фиг. 23.1. Опростения, използвани за изчисляване на нискотемпературната специфична топлина на хармоничен кристал.
(a) Типични дисперсионни криви на нормални режими на двуатомен кристал по някаква посока в k-пространството (с доста висока симетрия, тъй като два акустични и два оптични режима са изродени).
b - спектър, заместващ кривите, показани на фиг.а, при изчисляване на интеграла (23.15). Акустичните клонове се заменят с прави линии, простиращи се безкрайно в областта на произволно големи стойности на k (т.е. интегрирането върху първата зона на Брилуен се заменя с интегриране върху цялото k-пространство); оптичните разклонения се пренебрегват в този случай. Такива опростявания са оправдани, тъй като честотите, които са големи в сравнение с kv T/ħ (частите от дисперсионните криви на фигури a и b, лежащи над хоризонталната пунктирана линия), имат пренебрежимо малък принос към интеграла (23.15), ичастите от дисперсионните криви, съответстващи на режимите, които действително допринасят за количеството (23.15) (участъци от кривите под хоризонталната пунктирана линия), на фиг. a и b съвпадат. Квантова теория на хармоничния кристал 85
……………….. при много ниски температури имаме
(23.20)
За да бъде формула (23.20) валидна, е необходимо стойността на kvT/ħ да бъде малка в сравнение с всички фононни честоти, които не лежат в линейната част на спектъра; оттук следва, че стойността на kvT/ħ трябва да бъде малка част от характеристичната честота на границите на зоната. За да се изпълни това условие, температурата T трябва да бъде значително по-ниска от стайната температура. Тъй като когато температурата се понижи под стайната температура, законът на Дюлонг и Пети започва да се нарушава,има доста широк температурен диапазон, в който не са приложими нито нискотемпературни, нито високотемпературни изчисления,и трябва да се използва общатаформула (23.15). На практика обаче методите на интерполация често се използват в този междинен температурен диапазон.
ТОПЛИНЕН КАПАЦИТЕТ ПРИ СРЕДНИ ТЕМПЕРАТУРИ. МОДЕЛИ НА ДЕБАЙ И АНЩАЙН
Първите квантови изчисления на топлинния капацитет на решетката от Айнщайн и Дебай не използват фононния спектър в неговата обща форма, обсъдена по-горе, но приемат, че законът за дисперсия на нормалния режим има някаква особено проста форма. Резултатите от тези изчисления, базирани на грубо приближение на закона за дисперсия на нормалния режим, сега се използват като формули за интерполация. Освен това теорията на Дебай оказва значително влияние върху приетата терминология и дори определя начина, по който се представят експерименталните данни.
ИНТЕРПОЛАЦИОННА СХЕМА НА ДЕБАЙ
В модела на Дебай всички клонове на вибрационния спектър са заменени от три клона с едини същия линеен закон на дисперсия 3)
Освен това във формула (23.15) вместо интеграла върху първата зона на Брилюен се взема интеграл върху сфера с радиус kD, избрана така, че тази сфера да съдържа точно N разрешени вълнови вектора, където N е броят на йоните в кристала. Тъй като обемът на k-пространството на вълнов вектор е (2π) 3 /V (вижте том 1, стр. 50), това означава, че количеството (2π) 3 N/V трябва да бъде равно на 4π kD 3 /3 и следователно kD се определя от съотношението1)
(23.22)
След тези опростявания формулата (23.15) приема формата
(23.23)
При изчисляване на интеграла в (23.23) е удобно да се определи честотата на Дебай
и температура на Дебай
Лесно е да се види, че 1/kDхарактеризира средното разстояние между частицитев кристал, честотатаωDе от порядъка на максималната фононна честота,aθDе характерна температура; над неговсички режими са възбудени, а отдолу някои режими започват да „замръзват“
2).Нека направим промяна на променливите ħck/kBT = x; тогава формулата (23.23) ще включва само температурата на Дебай:
Тази формула изразява специфичната топлина при всички температури по отношение на един емпиричен параметър θD. Разумен начин за избор на θD (въпреки че в никакъв случай не е единственият използван) е да се изисква изразът (23.26) да е в съответствие с наблюдаваната специфична топлина при ниски температури. Това ще бъде осигурено (поне в хармонично приближение), ако връзката на скоростта c във формули (23.21) или (23.25) с точния фоно спектър е описана с формула (23.18).Полученият израз за нискотемпературния топлинен капацитет е:
(23.27)
а) Температурите на Дебай бяха определени чрез напасване на наблюдаваните специфичнитоплинни мощности Cv към формулата на Дебай (23.26) в точката, където Cv = 3nkB/2. Данните са взети от статията на de Launay [3].
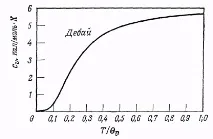
Фиг. 23.3. Зависимост на специфичната топлина в приближението на Дебай от T/θD. (от [3].)
температурата на Дебай играе същата роля в теорията на вибрациите на решетката, както температурата на Ферми играе в теорията на електроните в металите: и двете са характерни температури,отделящи нискотемпературната област, къдетоквантовата статистика,от високотемпературната област,където е валиднакласическата статистическа механика. Въпреки това,в случая на електрони, реалните температури винаги са много по-нискиTF,. докато температурата на Дебай θD (вижте таблица 23.3) обикновено е от порядъка на 10 2 K, така че можем да срещнем както квантови, така и класически режими.
Кратко обяснение на температурата на Дебай.
ТЕОРИЯ НА ДЕБЯ за твърдото тяло - теория, която описва трептенията на кристалните. решетки и дължащата се на тях термодинамика. свойства на твърдото тяло; предложен от P. Debye през 1912 г. във връзка с проблема за топлинния капацитет на кристала. D. t. се основава на опростено представяне на твърдо тяло като изотропна еластична среда, чиито атоми осцилират в краен честотен диапазон.
Кристален решетка, състояща се от N елементарни клетки с v атома, всяка има 3Nv-6 ≈ 3Nv вибрации. степени на свобода. С механични гледна точка, такава система може да бъде описана като набор от 3Nv независими осцилатори, всеки от които
ЗАКОН НА ДЕБЯ ЗА ТОПЛИННИЯ КАПАЦИТЕТ - теоретично изведен от П. Дебай през 1912 г. ф-ла, според който топлинният капацитет С на твърдо тяло при ниска темп-pax Т е пропорционален. куб temp-ry:
C = 2/5 π 2 kV (kT/ ћ c) 3 ( 1 )
където V е обемът, c е cf. скорост на звука. При ниски температуриpax, възможно е да не се прави разлика между топлинния капацитет при пост, обем Cv и пост, налягане Cp, тъй като в този случай Cp
За всички твърди вещества при T
0, топлинният капацитет на решетката се описва задоволително от f-loi ( 1 ). Това се дължи на факта, че при ниски temp-pax приближението на Дебай (виж теорията на Дебай) съответства на естеството на трептенията. спектър на твърдо тяло: съществуването на три акустични. вибрационни клонове Разликата се проявява в близост до температурните граници Tgr на приложимостта на теорията на Дебай. За прости кристални решетки (елементи и прости съединения) от порядъка на няколко. десетки K. За по-сложни решетки, както и за анизотропни структури (например квази-двумерни и квази-едномерни структури),
Когато сравнявате експерименти. резултати с D. h. т.е. има се предвид само топлинният капацитет на решетката, а нейните електронни и други компоненти са изключени (вижте топлинния капацитет).
Лит. виж чл. Теория на Дебай.
ТЕМПЕРАТУРА НА ДЕБАЙ – характеристика. температура на твърдото тяло, въведена от съотношението:
където ωD е max, честотата на трептене на кристала. решетка, определена от условията на равенство на броя трептения за честотен интервал от 0 до ωD, общият брой трептения. степени на свобода на решетката (виж теорията на Дебай).