Общи физически принципи на предаване на сигнал по оптично влакно - Студопедия
1.1. Структура на влакната
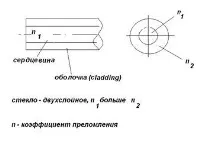
Фиг.1.1. Структура на влакната
Съвременното влакно има двуслойна структура: сърцевина с диаметър от няколко до няколко десетки микрометра и външен слой с диаметър 125 микрона или повече (фиг. 1.1). Както ще бъде показано по-долу, за нормално предаване на сигнала индексът на пречупване на сърцевината трябва да бъде по-голям от индекса на пречупване на външния слой: n1>gt; n2. В българската литература външният слой се нарича „обвивка“, въпреки че всъщност върху двуслойното стъкло има още няколко покрития, които представляват истинска изолационна обвивка. В англоезичната литература външният слой стъкло се обозначава с термина "cladding" ("masonry").
Коефициентът на пречупване във влакното може да се промени рязко при пресичане на границата
между обвивката и сърцевината и такова влакно се нарича стъпаловидно. Ако индексът на пречупване в сърцевината не остава постоянен, но се променя плавно, например по парабола, тогава такова влакно се нарича градиентно влакно (фиг. 1.2).
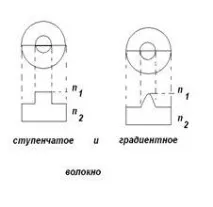
Фиг.1.2. Профил на индекса на пречупване
Коефициентът на пречупване се определя от формулата
където ε и μ са относителната диелектрична проницаемост и пропускливост на влакнестия материал. Тъй като за стъкло μ = 1, тогава n = ε 1/2.
1.2. отвор за влакна
Светлината, влизаща във влакното от края под определен ъгъл, преживява вътре в влакното
отражение и пречупване (фиг. 1.3).
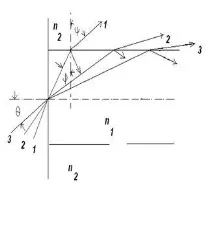
Да разгледаме, например, пътя на лъча 1. Под ъгъл φ спрямо вертикалата лъчът се доближава до границата между сърцевината и обвивката, където част от светлината се пречупва под ъгъл ψ и преминава в обвивката, а част се отразява и остава всърцевина. Ако намалим ъгъла θ между лъча и оста на влакното (лъч 2), тогава ъгълът ψ ще се увеличи и пречупеният лъч ще се разпространи по-близо до повърхността на сърцевината. Ъгълът ψ ще бъде още по-голям в случай 3 и пречупеният лъч в обвивката ще се разпространява почти успоредно на повърхността на сърцевината. С по-нататъшно намаляване на ъгъла на влизане θ до θ = θcr ще настъпи момент, когато ъгълът на пречупване ψ = 90º и пречупеният лъч ще се разпространи по повърхността на сърцевината и няма да навлезе в обвивката. Оттук нататък за θ
Ако имаме пълно вътрешно отражение, тогава ψ = 90 º и sin ψ = 1, тогава sin φ = n2 / n1 , a cos φ = (n1 2 - n2 2 ) 1/2 / n1 , откъдето
sin θ cr = (n1 / n0) ∙ (n1 2 - n2 2) 1/2 / n1 = (n1 2 - n2 2) 1/2. Тъй като този ъгъл е малък,
θcr ≈ sin θcr = (n1 2 - n2 2 ) 1/2 = NA (числова апертура - цифрова апертура).
Ако лъчът е въведен под ъгъл, по-малък от θcr, тогава във влакното има режим на пълно вътрешно отражение и лъчът се разпространява изцяло по сърцевината на влакното, нищо не излиза, докато апертурата на влакното е равна на
1.3. Концепцията за дисперсия
Когато се разпространява по влакното, сигналът изпитва затихване и разтягане (фиг. 4).
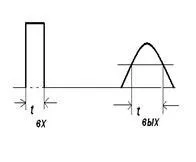
Фиг.1.4. Затихване и разтягане на сигнала по време на разпространение по влакното
Ако на входа на влакното имаме правоъгълен импулс, то след изминаване на определено разстояние на изхода имаме камбанообразен импулс, чиято продължителност обикновено се определя на ниво 0,5.
Стойността τ = се нарича дисперсия на сигнала във влакното. На практика това означава разтягане на сигнала след преминаването му през влакното. Дисперсията е много важна, защото ограничава скоростта на предаване на сигнала (фиг. 1.5).
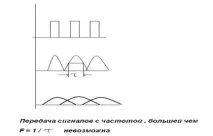
Фиг.1.5. Деформация на поредица от сигнали приразмножаване на влакна
При висока скорост (честота) на предаване на сигнала, в резултат на дисперсия, сигналите започват да се сливат и предаване с честота по-висока от 1/τ е невъзможно.
1.4. Разпространение на светлина през влакно
Разпространението на светлинните лъчи по стъпаловидни и градиентни влакна е показано на фигури 1.6 и 1.7. Предполагаме, че и двата лъча на тези фигури изпитват пълно вътрешно отражение. Два лъча излизат от една и съща точка като разширяващ се конус и навлизат в края на влакното под различни ъгли. Кой от тях на фигура 1.6 ще стигне пръв до изхода?
Фиг.1.6. Разпространение на светлината по стъпаловидно влакно
В стъпаловидно влакно скоростта на лъчите в сърцевината е еднаква и е равна на v = c / n1, където c е скоростта на светлината във вакуум. Тъй като лъч 1 има по-къс път, той ще стигне до изхода пръв; лъч 2 ще пристигне по-късно и ще има дисперсия на сигнала. Помислете сега за Фиг. 7: същите два лъча се разпространяват по градиентното влакно. Тъй като индексът на пречупване в сърцевината на градиентното влакно непрекъснато се променя, лъчите изпитват непрекъснато отклонение. В този случай лъч 1 върви
Фиг.1.7. Разпространение на светлината по градиентно влакно
близо до ядрото, където индексът на пречупване е приблизително равен на n1, а скоростта на разпространение е v1 = c/n1. Лъч 2 се движи повече по периферията на влакното по-близо до ръба, където индексът на пречупване е n2 и скоростта на разпространение е v2 ≈ c/n2. Лъч 1 поема по къс път, но скоростта му на разпространение е по-бавна, докато лъч 2 поема по-дълъг път, но с по-висока скорост, тъй като n1>gt; n2. В резултат на това двата лъча достигат до изхода приблизително едновременно и дисперсията в градиентното влакно е значително по-малка, отколкото при същото напречно сечение в стъпаловидно влакно.
1.5. Понятието мода.
Светещвълната в пространството има определена дължина на вълната, в рамките на която се променят векторите на електрическото и магнитното поле. Вълната може да има различни размери и форми, както и да бъде различно ориентирана по отношение на избраната координатна система на средата за разпространение, тоест поляризирана. Възможно е също така да има различна връзка между дължината на вълната и напречните размери на средата за разпространение. Светлината в сърцевината на влакното може да се разпространява само под определени ъгли, когато въведените вълни се усилват по време на добавянето им и възниква така наречената конструктивна интерференция. Типът вълна, характеризираща се с определена пространствена и времева структура, която може да се разпространява в оптично влакно, се нарича мода. Математически разрешените режими могат да бъдат получени чрез решаване на уравненията на Максуел за оптично влакно, като се вземат предвид граничните условия. Може също да се каже, че модата е естествена вълна, която има напречно разпределение на полето, независимо от посоката на разпространение. В случай на влакно най-простият режим е вълна с надлъжни линии на електрическо поле, разположени по дължината на влакното (фиг. 1.8), и линии на магнитно поле, които са концентрични кръгове в сечението на влакното.
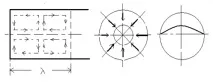
Фиг.1.8. Най-простият случай на поставяне на режим във влакно
Линиите на електрическото поле по дължината на влакното са показани с пунктирани линии. В края на влакното линиите на електрическото поле са линии, насочени в този случай към оста на влакното. Магнитните силови линии в напречното сечение на този режим са концентрични кръгове (не са показани на чертежа). Фигура 1.8 показва по същия начин как величината на електрическото поле се променя по протежение на секцията на влакното в този случай. Това е пример за вълна, в която електрическото поле е надлъжно, а магнитното поле енапречно. Но може да бъде и обратното, когато магнитното поле е надлъжно, а електрическото поле е напречно. Няколко периода могат да бъдат поставени в сечението (вижте например фиг. 1.9), а вълната може да бъде (в повечето случаи) хибридна, когато има както надлъжни, така и напречни компоненти както на електрическите, така и на магнитните полета.
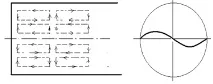
Фиг.1.9. Моден пример.
Важно е да се отбележи, че броят на полуциклите, разположени в секцията с влакна, трябва да бъде цяло число. Не може да има режим с нецяло число полупериоди в напречното сечение на влакното. Такъв режим ще се разпадне на режими с по-малък полупериод. Обикновено може да има много режими във влакното. Ако намалите диаметъра на влакното, тогава можете да стигнете до такъв размер, когато във влакното остава само една мода с дадена дължина на вълната. Такова влакно се нарича едномодово.
1.6. видове влакна.
По този начин, според профила на индекса на пречупване, има три основни вида влакна: стъпаловидни, градиентни и едномодови. Профилите на индекса на пречупване на стъпаловидни и градуирани влакна са показани на фиг. 1.2. Курсът на кривата на индекса на пречупване на градуирано влакно обикновено е парабола. Диаметърът на сърцевината на многомодовите стъпаловидни и градуирани влакна е 50 µm, а общият диаметър на влакното е 125 µm. Стандартите също така позволяват производството на многомодови влакна с диаметър на сърцевината 65 µm. Едномодовото влакно в класическата си версия е стъпаловидно влакно, но диаметърът на сърцевината е около 10 микрона. Едномодовото влакно има значително по-ниска дисперсия дори в сравнение със степенуваното влакно, което ще бъде обсъдено в следващия раздел. Стандартите позволяват производството на влакна с други параметри за редица специфични случаи, например оптични системи на самолети и др. ОТНОСНОнякои други видове влакна, по-специално влакна, направени от полимери, халкогенидни стъкла и фотонни кристали, ще бъдат обсъдени по-късно.
Не намерихте това, което търсихте? Използвайте търсачката: