Общобългарски интернет конкурс за педагогическо творчество
Професионален конкурс за педагози
ЦЯЛ БЪЛГАРСКИ ИНТЕРНЕТ - СЪСТЕЗАНИЕ
ПЕДАГОГИЧЕСКО ТВОРЧЕСТВОДЪРЖАВНА БЮДЖЕТНА УЧЕБНА ИНСТИТУЦИЯ ЗА СРЕДНО ПРОФЕСИОНАЛНО ОБРАЗОВАНИЕ
"ШАХТИНСКИ ПЕДАГОГИЧЕСКИ КОЛЕЖ"
Педагогически идеи и технологии: професионално образование
ЕЛЕМЕНТИ НА ТЕОРИЯ НА МНОЖЕСТВАТА В ИЗУЧАВАНЕТО НА МАТЕМАТИКАТА
(Учебник)Съставител: Руд Елена Владимировна, учител по математика
Място на изпълнение на работата: ГБОУ СПО РО "ШПК",
346500, Ростовска област, Шахти, ул. Шевченко, 151.Мини
1. Теоретична информация за някои раздели на теорията на множествата
1.1. Основни понятия и определения…………………………………………..5
1.2. Начини за определяне на множества…………………………………………. 6
1.4. Връзки между множества………………………………………………………………………………………………………………………………………………………………………………………………
1.5. Операции върху множества …………………………………………. 9
1.6. Броят на елементите на комплекта……………………………………………………..11
1.7. Декартово произведение на множества…………………………………………..13
1.8. Изобразяване на декартово произведение на две числови групи
на координатната равнина……………………………………………..15
1.10. Начини за установяване на взаимоотношения………………………………………. 20
1.12. Концепцията за съответствие………………………………………………. 25
1.13. Съответствие, обратно на това……………………………………………27
1.14. Кореспонденции едно към едно………………………………………..29
2. Практически задачи към някои глави от теорията на множествата
2.1. Практически упражнения по темата „Методи за специфициране на множества.
Операции върху множества”…………………………………………….30
2.2. Практически упражнения по темата „Декартово произведение
комплекти. Графично представяне на декартововърши работа"……. 32
2.3. Практически упражнения по темата „Връзки между елементи
комплекти. Начини за установяване на взаимоотношения”……………………………. 34
2.4. Практически упражнения по темата “Свойства на връзката”…………. 35
2.5. Практически упражнения по темата „Кореспонденция.
Кореспонденции едно към едно”………………………………. 36
ВЪВЕДЕНИЕМатематиката играе важна роля в цялостната образователна система. За продуктивна дейност в съвременния информационен свят е необходима достатъчно силна базова математическа подготовка.
Математиката, която отдавна се е превърнала в език на науката и технологиите, сега все повече навлиза в ежедневието и ежедневния език и все повече се въвежда в области, традиционно далеч от него.
Интензивното математизиране на различни области на човешката дейност се засили особено с появата и развитието на компютрите. Математическата грамотност на човек се изисква буквално на всяко работно място. Това предполага специфични математически познания.
Математиката допринася за формирането на общата култура на човека. Изучаването на математика допринася за естетическото възпитание на красотата и изяществото на математическите разсъждения; развива въображението, пространствените представи. Историята на развитието на математическите знания дава възможност да се попълни запасът от исторически и научни знания, да се формира в тях представа за математиката като част от универсалната култура.
Тази статия очертава елементите на интуитивната теория на множествата, която е необходима за разбирането на всеки клон на математиката, тъй като всеки от тях се основава на интуитивната теория на множествата и предполага свободно владеене на концепциите за двоична връзка и съответствие.
Предлаганото ръководство може да се използва както за работа под ръководството на учител,и за самостоятелно изучаване на елементите на теорията на множествата.
1. ТЕОРЕТИЧНА ИНФОРМАЦИЯ ЗА НЯКОИ РАЗДЕЛИ ОТ ТЕОРИЯ НА МНОЖЕСТВАТА
1.1. ОСНОВНИ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯВ българския език обикновено се използват различни думи за означаване на определени множества. Например, те казват: стадо крави, стадо коне, букет цветя, екип от спортисти, набор от инструменти, колекция от печати и др. В математиката се стремят към еднаквост и като правило за обозначаване на колекциите се използва един термин -множество. По този начин наборът се разглежда като колекция от обекти от реалния свят (или обекти на нашата интуиция), които имат общо свойство. С други думи, наборът е съвкупност от обекти, считани за един обект. Невъзможно е да се даде определение на набор, може само да се обясни.
Понятието набор е едно от основните понятия на математиката и следователно не се дефинира по отношение на други. Може да се обясни с примери. И така, можем да говорим за набор от гласни на българската азбука, набор от естествени числа, набор от триъгълници, набор от корени на уравнение и т.н.
В разговорната реч терминът "комплект" винаги се свързва с голям брой обекти. В теорията на множествата това не е необходимо. Ще разгледаме кактобезкрайнимножества, така и множества, съдържащи произволенкраенброй обекти, и дори множество, което не съдържа нито един обект -празно множество (означено с∅).
Обектите, които съставляват набора, го наричат елементи.
Връзката между елементи и набор се изразява с думите: „е елемент“ или „принадлежи“. Изречението "Елементaпринадлежи на множество A" е означено с

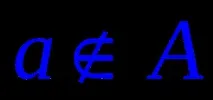
Набори, чиито елементи са числа, се наричат числови. За числови набори се използва общоприетата нотация:
N е множеството от естествени числа;
Z е набор от цели числа;
Q е множеството от рационални числа;
R е множеството от реални числа.1.2. МЕТОДИ ЗА ОЗНАЧАВАНЕ НА МНОЖЕСТВАМножеството може да се счита за дадено, ако е възможно да се каже за всеки обект дали той принадлежи към това множество или не.
Набор може да бъде дефиниран чрездиректно изброяванена всички негови елементи в произволен ред. В този случай имената на всички елементи на множеството се записват в низ, разделени със запетаи и оградени във къдрави скоби. Всеки елемент се записва само веднъж. Редът, в който са изброени неговите елементи, не е от значение.
Например множеството A, състоящо се от всички цифри, може да бъде записано като:
Наборът P от букви, които използват думата "математика" за писане, се записва, както следва:
и са един и същ комплект.
Изброяването на елементи може да дефинира само краен набор с малък брой елементи. Когато е трудно или невъзможно (в случай на безкрайни множества) да се уточни множество чрез изброяване на неговите елементи, тогава се използва друг начин за уточняване на множеството чрез указване на характерното свойство на неговите елементи.
Характерно свойство, което дефинира набор, е свойство, което притежава всеки елемент, принадлежащ към даденото множество, и нито един елемент, който не му принадлежи.
Например писане B = Z, -2