Оптимизация на портфолио с помощта на модела на Марковиц
Моделът се основава на факта, че показателите за доходност на различни ценни книжа са взаимосвързани: с нарастването на доходността на някои ценни книжа има едновременно увеличение на други ценни книжа, третите остават непроменени, а на четвъртите, напротив, доходността намалява. Този тип зависимост не е детерминистична, т.е. уникално определена и стохастична и се нарича корелация.
Моделът на Марковиц има следните основни допускания:
—доходносттана ценна книга се приема катоочакване за доходност;
—рискътна ценна книга естандартното отклонение на възвращаемостта;
— предполага се, че данните заминалитепериоди, използвани при изчисляването на възвръщаемостта и риска, отразяват напълнобъдещитестойности на възвръщаемостта;
— степента и естеството на връзката между ценните книжа се изразявачрез линеен корелационен коефициент.
Според модела на Марковиц възвръщаемостта на портфейл от ценни книжа е среднопретеглената възвръщаемост на ценните книжа, които го съставят, и се определя по формулата:
където N е броят на ценните книжа в портфейла;
— процентния дял на тази ценна книга в портфейла;
е добивът на дадена хартия.
Рискът на портфейл от ценни книжа се определя от стандартното отклонение на възвръщаемостта на портфейла:
,
където , - процентни дялове на тези ценни книжа в портфейла;
, — риск от тези ценни книжа (стандартно отклонение);
е коефициентът на линейна корелация.
Използвайки модела на Марковиц за изчисляване на характеристиките на портфейла, прекият проблем става:
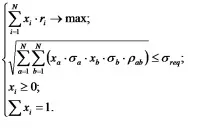
Обратната задача се представя по подобен начин:
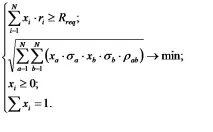
При практическото приложение на модела на Марковиц за оптимизиране на портфолио от акции,следните формули:
1) доходността на ценна книга:
,
където T е броят на минали наблюдения на възвръщаемостта на тази ценна книга.
2) рискът от ценна книга (под формата на оценка на стандартното отклонение):
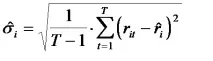
3) статистическа оценка на коефициента на корелация между показателите за доходност на две ценни книжа:
,
— доходност на ценни книжаaиbв периодаt.
Ясно е, че за N разглеждани ценни книжа е необходимо да се изчисли
коефициенти на корелация.
Нека проведем числена симулация на оптимизация на портфейла от акции, използвайки модела на Марковиц за изчисляване на характеристиките на портфейла. Дори при използване на оптимизационния модел е невъзможно ръчно да се избере оптималното портфолио. За решаване на проблема с оптимизацията беше използвано приложение за електронни таблици EXCEL, наречено Solver („търсене на решения“).
Възвръщаемостта на ценните книжа е основно сумата от
- капитализирана доходност, свързана с промени в пазарната цена на ценните книжа,
- дивидент или лихвен доход.
Ще покажем имплементацията на модела в ET Excel. Първо, ние избираме данни за тези акции, които отговарят на принципа на Парето.
Ние организираме изчисляването на целевата функция в Excel

| ТРАНСПОНИРАНЕ (B70:B76) |
| SUMPRODUCT(D87:J87; D88:J88) |
Нека изчислим коефициентите на ковариация между възвръщаемостта на акциите, които сме избрали:
Пакет за анализ на данни - Ковариация. (Вижте снимката)
Резултатът ще бъде ковариационна матрица, получена в следната форма:
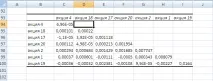
След това ще трябва да извършим умножение на матрица, за това е необходимо в получената матрица да няма „празни“ клетки. Забележкаче матрицата е симетрична спрямо главния диагонал, така че трябва да получите съответните стойности в "празните" клетки. Как да го направим?
Една от възможностите е да транспонирате оригиналната матрица с помощта на функцията TRANSPOSE
| =(D94+D103) |
| =(C94+C103)/2 |
| TRANSPOSE(C94:I100) И натиснете CTRL+SHIFT+Enter |
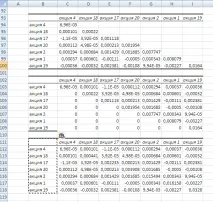
След това, за да изчислим портфейлния риск, правим следното:
| ТРАНСПОНИРАНЕ (D88:J88) |
Сега нека добавим ограничения към модела, както е показано на фигурата по-долу.
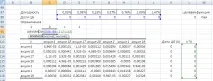
И накрая, според модела на Марковиц, имаме
Следващият етап е оптимизация, която се извършва с помощта на инструментаData-Search for a solution. Нека покажем как да го направим технически.
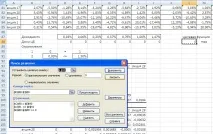
Най-накрая имаме следната оптимизация
Това означава, че 34,4% от паричните инвестиции трябва да бъдат инвестирани в акции с доходност от 1,00% и 65,59% в акции с доходност от 1,47%, в нашата нотация това са акции 1 и акции 19
Като първоначални данни за моделиране бяха използвани седмичните котировки на акции на шест украински предприятия за определен период. Таблица 1 представя данни за възвръщаемостта на акциите през разглеждания период, като възвръщаемостта е равна на относителния ръст (намаление) на котировките.
Въз основа на данните в табл. 4.9.1 се изчисляват доходността (математическо очакване) и рискът (стандартно отклонение) на всяка ценна книга. Резултатите от изчисляването на доходността и риска на ценните книжа са представени в табл. 4.9.2. В табл. 4.9.3 изчислени коефициенти на линейна корелация между доходността на ценните книжа.
Раздел. 4.9.1. Първоначални данни за доходността на ценните книжа
| НОМЕР НА ПЕРИОДА | ||||||||
| Вреднохартия: | ||||||||
| Промоции 1 | -1,25% | 0,00% | 4,43% | -12,12% | 32,41% | -5,21% | -17,58% | 14,00% |
| Промоции 2 | -15,56% | 0,00% | 72,11% | 10,86% | 22,76% | 1,12% | 6,67% | -8,33% |
| Промоции 3 | 11,24% | 0,00% | 19,79% | 17,39% | -4,07% | 4,25% | -25,93% | -9,00% |
| Промоции 4 | 0,00% | 0,00% | 2,30% | 1,12% | 0,00% | 0,00% | 16,56% | 0,00% |
| Промоции 5 | -0,85% | 14,89% | 33,59% | -27,09% | 0,12% | 23,29% | -4,41% | 2,62% |
| Промоции 6 | 47,37% | -11,90% | -9,46% | 4,48% | 22,00% | -4,92% | -3,33% | -8,66% |
| НОМЕР НА ПЕРИОДА | ||||||||
| Ценни книжа: | ||||||||
| Промоции 1 | 0,00% | -3,46% | -10,00% | 30,00% | 1,23% | -8,97% | -1,45% | |
| Промоции 2 | 1,14% | 3,45% | 5,20% | -7,65% | -13,21% | 2,76% | 8,52% | |
| Промоции 3 | 23,08% | 10,60% | 0,98% | 0,00% | 12,34% | 0,00% | -34,00% | |
| Промоции 4 | 0,00% | 5,76% | 1,54% | -0,70% | 0,00% | -1,46% | -12,51% | |
| Промоции 5 | 0,32% | 13,40% | 4,70% | 0,00% | -23,51% | 9,43% | 3,01% | |
| Промоции 6 | -3,77% | -1,20% | 0,00% | 32,10% | 17,30% | 2,01% | -1,92% |
Раздел. 4.9.2. Възвръщаемост и риск на разглежданите ценни книжа
| Доходност | Риск | |
| Промоции 1 | 1,47% | 14,18% |
| Промоции 2 | 5,99% | 20,72% |
| Промоции 3 | 1,78% | 15,85% |
| Промоции 4 | 0,84% | 5,76% |
| Промоции 5 | 3,30% | 15,45% |
| Промоции 6 | 5,34% | 16,93% |
При численото моделиране изискваната възвръщаемост на портфейла беше зададена на 4%, приемливият риск на портфейла беше 8%. С помощта на вградената функция на процесора за електронни таблици Excel Solver „търсене на решение“ бяха решени преки и обратни задачи за оптимизиране на портфолиото от акции. След обработка на данните от разглежданите ценни книжа бяха изчислени оптималните структури на портфейла, осигуряващи максималната възможна доходност за дадено ниво на риск (директен проблем) или минимално възможен риск за дадена доходност (обратен проблем). Получените резултати са представени в табл. 4.9.4.
Раздел. 4.9.3. Коефициенти на корелация между доходността на ценните книжа
| Промоции 1 | 0,06 | 0,01 | -0,30 | 0,06 | 0,41 |
| Промоции 2 | 0,15 | 0,08 | 0,50 | -0,37 | |
| Промоции 3 | 0,08 | 0,01 | 0,14 | ||
| Промоции 4 | -0,03 | -0,11 | |||
| Промоции 5 | -0,40 | ||||
| Промоции 6 |
Раздел. 4.9.4. Оптимални портфейлни структури според модела на Марковиц
| Структура на портфолиото | ||
| Директен проблем | Обратна задача | |
| Изисквания: | Риск по-малък от 8% | Доходност над 4% |
| Промоции 1 | 0% | 0% |
| Промоции 2 | 26% | 20% |
| Промоции 3 | 0% | 0% |
| Промоции 4 | 10% | 24% |
| Промоции 5 | 19% | 18% |
| Промоции 6 | 45% | 38% |
| Характеристики | Доходност 4,68% | Добив 4% |
| оптимално портфолио | риск 8% | Риск 6,65% |
Основният недостатък на модела на Марковиц е, че очакваната възвръщаемост на ценните книжа се приема за равна на средната възвръщаемост за минали периоди. Следователно моделът на Марковиц е рационален за използване пристабилно състояние на фондовия пазар, когато е желателно да се формира портфейл от ценни книжа от различен характер, с повече или по-малко дълъг живот на фондовия пазар.
Тази страница е последно модифицирана: 2016-07-23