Относно 2D опаковкатаонлайн алгоритми, SavePearlHarbor

Още едно копие на пристанището

Главно меню

Навигация на публикации

Относно двуизмерното опаковане: онлайн алгоритми

Същността на проблема: имаме полу-безкрайна лента - като в Tetris, само че без края на играта, и краен набор от правоъгълници. Данните за правоъгълник се получават в реално време; всеки нов правоъгълник трябва да бъде поставен веднага и да не се мести отново. Целта е да се сведе до минимум общата височина на пакетираните правоъгълници. Това е онлайн вариант на проблема с 2DSP (2DSP).

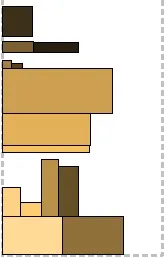
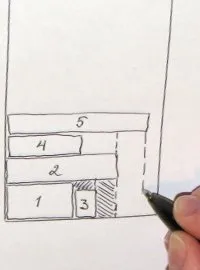
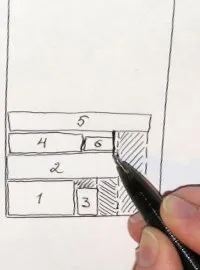
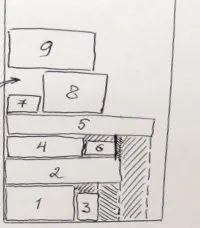
Малко повече теоретична информация можете да намерите в предишната статия, но засега, без повече шум, нека преминем към алгоритмите. Следната последователност от тухли ще бъде използвана за илюстративни цели: (Изходни данни, спонсорирани от random.org). Ще бъдат описани някои евристични алгоритми, чиято обща идея е предварително да разделят лентата на региони и да поставят новопристигнали правоъгълници в конкретен регион според определени критерии.

Алгоритми за ниво

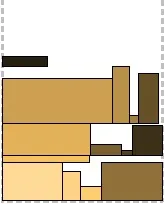
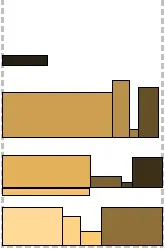
Подходът на всички алгоритми за нива е, че лентата е разделена на нива въз основа на височината на правоъгълниците, налични на този етап. Правоъгълниците се поставят по дъното на текущото ниво отляво надясно, колкото е възможно по-дълго; правоъгълникът, който не пасва, се пакетира на следващото ниво. Височината на всяко ниво се определя от най-високия правоъгълник в него. Ето три опции за опаковане: Next Fit Level - когато се отвори следващото ниво, предишното се "затваря" и вече не се взема предвид; Първо ниво на годност - на всяка стъпка от алгоритъмавсякониво се разглежда, като се започне от най-ниското и правоъгълникопакова се на първия подходящ, на който има достатъчно място; Ниво на най-добро прилягане — на всяка стъпка от алгоритъма се преглеждатвсичкинива и се избира най-подходящото — това, което оставя най-малко място след опаковането. И трите алгоритъма са илюстрирани по-горе. На този етап е лесно да се познае кой къде се намира.

Първо ниво на годност

Двустепенно следващо прилягане

Хитра модификация на Next Fit Level. Нивата са създадени в две, всяко от които има своя собствена стратегия. По-ниско ниво (или всички нечетни): Първият пристигнал правоъгълник се пакетира отляво, останалите се пакетират отдясно наляво, стига да има достатъчно място. След това нивото се затваря и височината му се определя от най-високия правоъгълник в него. Най-горно ниво (или всички дори): ако има само един правоъгълник в долното ниво, нивото се пакетира по същия начин като долното. Ако са два или повече, тогава първият правоъгълник се набива върху долния от двата, притиснати към ръбовете на лентата, и също се притиска към ръба на лентата; всички следващи се пакетират отдясно наляво, независимо дали първият е бил пакетиран отляво или отдясно.

Звучи объркващо и не е веднага ясно защо такива танци с тамбура. Единственото нещо, което този алгоритъм очевидно осигурява, е по-равномерно разпределение на правоъгълниците по обема на лентата, без изкривяване към левия ръб. Но ние ще се върнем към тази стратегия, когато разглеждаме алгоритмите за компресиране.

Алгоритми на рафта

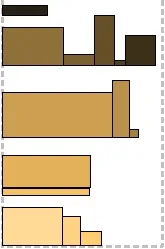
Алгоритмите на рафта не са обвързани с точната височина на правоъгълниците и след опаковането на първия на нивото (рафта) остава малко място, в случай че следващият е малко по-висок. Това "леко" се контролира от параметъраr∈ (0;1). Височината на рафта се определя катоrk, къдетоrk+1kза някакво цяло числоkи височина на първия опакован правоъгълник h(Li). Подобно на алгоритмите за ниво, се прилагат стратегиите за заобикаляне на рафта Next Fit, First Fit и Best Fit. „Резервът“, оставен на всеки рафт, става печеливш в последните два случая (сравнете FFL и FFS, BFL и BFS). В примераp=0.7.

Първи монтиран рафт

Хармоничен рафт

Harmonic Shelf пакетира правоъгълници с еднаква височина, но и с еднаква ширина. Резултатът ще бъде повече нива, но те ще бъдат запълнени по-плътно. Въвежда се допълнителен параметърMза изчисляване на допустимата ширина.

Общата честотна лента, за простота, ние я приемаме като единица, е разделена наMинтервалиI1..IM. Авторът твърди, че разумна стойностMе в [3; 12]. Ширината на интервалите се изчислява по формулата:

;

За всеки правоъгълник се изчислява стойностp. Параметърkза височина се изчислява подобно на алгоритмите за рафтове. Проверяват се две условия: дали има място за правоъгълника на някой рафт с височинаrkи дали отговаря на вече опакован тамp. Ако поне един от тях не е завършен, за него се създава собствен рафт, с блекджек и най-удобните условия. В примераp=0.7,M=4.

За разделяне на нива се въвежда определена прагова стойност 0j-1jи ширина 2 —x-1-xса опаковани в едно ниво. Тоест, нивото се характеризира с двойка (x,j) за някакво цяло числоjи естественоx.

Правоъгълници с ширина най-малкоYсе наричат ​​буфери всеки от тях е пакетиран на отделно ниво. Тоест, ако ви хванаттакъв правоъгълник, трябва спешно да отворите ново ниво, височина, равна на него. Всички останали (небуферирани) се пакетират в първото подходящо ниво. Подходящ - в смисъл със същата двойка (x,j). Ако внезапно няма достатъчно място, небуферен правоъгълник може да стане първият в ново ниво, тогава височината на това ниво ще бъде 2j. Като цяло някаква нездравословна йерархия. В примераY=0,4.

Алгоритми за компресиране

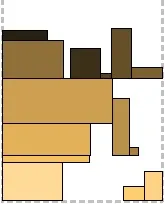
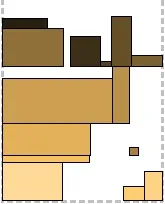
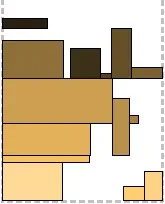
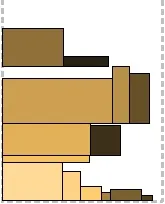
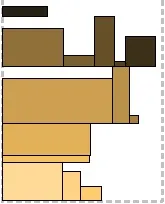
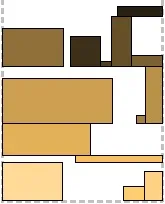
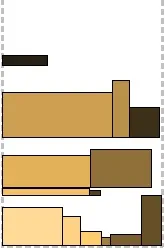
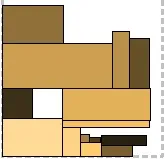
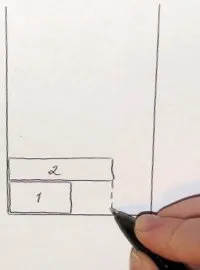
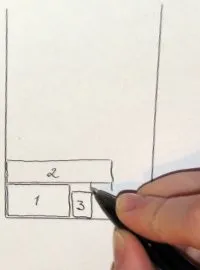
Алгоритмите за компресиране са базирани на BiNFL и по същество са корекции към метод за пакетиране от най-високо ниво. Общата разлика е, че най-горното ниво винаги е пакетирано отляво надясно. Напасване на частта за компресиране: За всеки правоъгълник, опакован до най-горното ниво, се проверява дали има място под него в долното ниво. Ако можете да го преместите на по-ниско ниво, така че част от него да остане на горното ниво, той се премества (следователно Part Fit - може да бъде частично "натиснат" в предишното ниво). По този начин може да се намали общата височина на второто ниво. По никакъв начин не засяга опаковката. На първата снимка можете да видите правоъгълник, висящ между нивата - той беше изместен. Пълно прилягане на компресията: За всеки правоъгълник, опакован до най-горното ниво, се проверява дали може да се побере напълно до предходното ниво. Всъщност, ако може, тогава се измества. Това ни дава стратегическо предимство: така освободеното място в нивото може да се използва за следващия правоъгълник. За съжаление втората рисунка не съдържа такава ситуация, но за сметка на това се виждат две неуспешни. Compression Combo: Да, да, това е комбинация от предишните две и съответно комбинация от техните плюсове. Третата фигура илюстрира.

Напасване на частта за компресия

Пълна компресияFit

Онлайн годни

По-отнемащ време метод от предишните, но и по-продуктивен. Въз основа на алгоритъма на Бърк за офлайн версията на проблема. Някои аспекти може би ще нарисувам.

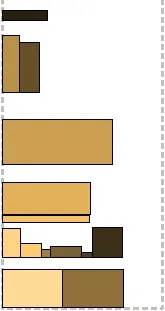
По време на процеса на опаковане могат да се образуват празни области (Empty Areas), които алгоритъмът ще се опита да запълни на първо място. Как могат да се оформят се вижда на снимката вляво. Имайте предвид, че за това трябва да съхраните определено представяне на пълнотата на лентата. След като се запълни, една празна област може да се превърне в две (или може да не се превърне в две).

Също така няколко региона могат да бъдат създадени наведнъж с една стъпка на опаковане - пространството под правоъгълника се анализира вертикално и се разделя на броя на "стъпките". Средната снимка отново показва разделянето на празната област на две след опаковането на правоъгълника там (между другото, струва ми се, че би било по-добре да го разделяхоризонталнона това място). Като цяло, колкото по-навътре в гората, толкова повече празнини. На всяка стъпка бързо свиващите се празнини се изследват внимателно. Тук виждам друга оптимизация: можете да въведете мярка за целесъобразната област и да изхвърлите нежеланите.

Ако не съвпада празна област, опаковането продължава с метода на Бърк. Спомням си. Изгражда се карта на височината за лентата и правоъгълникът се пробва в най-ниската зона в момента. Ако не влезе там, ниското място се "запълва" до нивото на най-близкото стъпало и търсенето се повтаря. Така едно потенциално място може да бъде избутано до самия връх, а след това има друга възможност за образуване на празно пространство (виж вдясно). Една и съща карта на височината се използва на всяка стъпка за идентифициране на празни зони.

Общо взето всичко вече е казано. Първо се опитваме да опаковаме празниобласти, след това до най-ниското място и накрая до върха, изроден случай на „най-ниско място“.

Послеслов

За да разсея усещането за безцелност на случващото се, ще дам един от класическите, но вдъхновяващи примери за прилагане на алгоритми за двумерно опаковане в полуограничена лента. Това е планировчик на задачи за многопроцесорна система. В съвременния софтуер за клъстери се използват повече "възрастни" алгоритми, но самата задача за планиране се свежда до 2DSP. При условията на клъстерна работа потокът от входящи задачи не е нищо повече от онлайн данни за опаковане: хоризонталното измерение е необходимия брой ядра, а вертикалното измерение е времето за изпълнение на задачата. (Всичко е като в зората на технологиите: стоите на опашка пред компютъра и предварително предупреждавате колко ресурси ви трябват и колко време ще се върти перфокартата ви). Планировчикът трябва да разпредели конкретни процесори за задачата и да определи кога да започне. В чистата си форма, между другото, не може да се използва алгоритъм, тъй като времето капе, докато планировчикът чака задача или мисли за нейното поставяне. Освен това програмистът може да бъде обвързан от различни специфични условия: приоритет на задачите; възможност за мащабиране на задачата по време на изпълнение; хардуерни закъснения и системно самообслужване, включително преразпределение, като се вземат предвид повредените ресурси; сравнение на характера на комуникациите в рамките на задачата с архитектурата на клъстера и др. Всеки алгоритъм е красив в своята математическа строгост, докато не започнете да го прилагате в реалния живот.

И накрая - сравнително описание на алгоритмите в приятна безлична форма. Тук е съотношението на оптималната височина на опаковката (сумата от площите на правоъгълниците, разделена на ширината на лентата) към получената.

---