Паралелна проекция
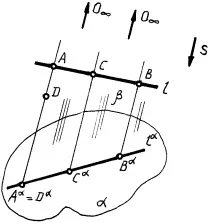
Специален случай на централна проекция с център на проекциите, разположен в безкрайност (в неправилна точкаO). Осъществява се от сноп лъчи от дадена посокаS(фиг. 2).
Апарат за паралелно прожектиране:
S— посока на проекцията;
A = [OA] е успоредна проекция на точка A върху равнината;
l = (AA BB ) е успоредна проекция на права линия върху равнината .
Няма обратимост. Една централна проекция на точка не позволява да се прецени позицията на точка в пространството. A =D
-
Инвариантни свойства на паралелната проекция
Геометричните фигури се проектират върху проекционната равнина, като цяло, с изкривяване. Естеството на изкривяването зависи от проекционния апарат и положението на проектираната фигура спрямо равнината на проекцията.
По-специално, по време на паралелна проекция се нарушават метричните характеристики на геометричните фигури (линейните и ъгловите стойности са изкривени). Някои свойства на фигурата се запазват върху нейната проекция.
Свойствата на фигурата, които се запазват в проекцията, се наричат независими или ИНВАРИАНТНИ. Тези инвариантни свойства често се наричат накратко инварианти.
Инварианти на паралелна проекция
Проекцията на точка е точка (фиг. 1; фиг. 2)
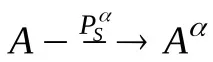
Проекцията на права линия е права линия (фиг. 1; фиг. 2)
3. Проекцията на точка, принадлежаща на права, принадлежи на проекцията.
тази права линия (фиг. 1; фиг. 2)
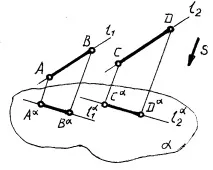
Проекцията на пресечната точка на линиите се определя от пресечната точка на проекциите на тези линии (фиг. 3)
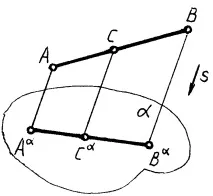
Проекциите на взаимно успоредни прави са взаимно успоредни (фиг. 4)
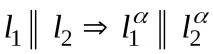
Отношението на дължините на отсечките на взаимно успоредни прави е равно на отношението на техните дължинипроекции (фиг. 4)
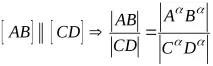
ПРАВИЛНО:ако отсечка е разделена на точка в произволно съотношение, тогава проекцията на отсечката е разделена на проекцията на тази точка в същото съотношение (фиг. 5)
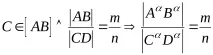
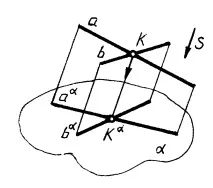
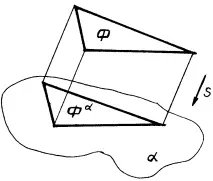
7. Плоска фигура, успоредна на равнината на проекциите, се проектира върху тази равнина в конгруентна фигура (фиг. 6)
Правоъгълна (ортогонална) проекция
Специален случай на паралелна проекция, при която посоката на проекцията е перпендикулярна на проекционната равнина (фиг. 7)
По-нататък безусловно се използва ортогонална проекция.
Ортографската проекция запазва всички свойства на паралелната проекция. Освен това за ортогонална проекция е валидна теоремата за проекцията на прав ъгъл (вижте тема № 6) и прилагаме метода за определяне на разстоянието между точките (т.е. дължината на отсечката, вижте тема № 3), наречен метод на правоъгълния триъгълник.
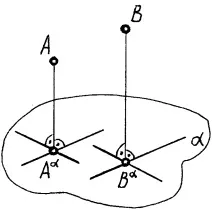
Позицията на даден обект в пространството се определя от неговите четири точки, които не лежат в една и съща равнина. Изображението на пространствен обект в чертежа се свежда до изграждането на проекции на набор от точки на този обект върху равнинатаR(наречена проекционна равнина) с помощта на прави линии (прожектиращи лъчи), минаващи през точките на обекта и насочени към центъра на проекциятаS.
Въпреки това, за да се изгради проекция на обект, не е необходимо да се изградят всички негови точки. Достатъчно е да се намерят само проекциите на характерни точки (върхове, ръбове и т.н.), които след това се свързват със съответна линия.
Издаващите се греди заедно образуватиздаваща се повърхност. И така, при проектиране на права линия AB, проектиращата повърхност е равнината ABba(фиг. ).
Пресечна линияabна проектиращата равнина с равнинатаRе проекцията на праватаAB, която е съставена от проекциите на нейните отделни точки.
Проекцията е като сянка, хвърлена от обект, осветен от лампа или слънце.
При проектиране на крива линия в първия случай, проектиращите лъчи образуват конична повърхност с връх в точкатаS; Във втория случай конусът на изпъкналите лъчи се превръща в цилиндър и коничното изображение става цилиндрично (успоредно) (фиг. 2). Проекцията на кривата линия се счита за линия на пресичане на проектиращата повърхност с равнинатаR.
В перспектива обектът се изобразява така, както изглежда за окото на наблюдателя. Лещата на окото е центърът на проекцията. Всеки от нас е запознат със следния феномен: ако погледнем по протежение на железопътната линия, ни се струва, че релсите сякаш се приближават една към друга и се събират на хоризонта в една точка (център), а опорите, разположени по протежение на релсите, намаляват, докато се отдалечават.
Паралелната проекция еспециален случай на перспектива. Същността на паралелната проекция е следната: ако условно премахнем центъра на проекцията до безкрайност, тогава проектиращите лъчи могат да се считат за успоредни.
И така, за да построите успоредна проекция на триъгълникаABC(фиг. ), трябва да посочите:R- равнината на проекцията (да не е успоредна и да не съвпада с посоката на проектиращите лъчи);S- посоката на проектиращите лъчи (посоката на проекцията).
Освен това проектиращите лъчиAa,BbиСссе прекарват през характерните точки на обекта, успоредни на посоката на проекцията, след което се намират точкитеa,bи от тяхното пресичане с равнинатаR.Тези точки са желаните успоредни проекции на точкитеA,BиCна дадения триъгълник.
Проекциятаabcе пресечната линия на проектиращата се призматична повърхност с равнинатаR. Формата и размерите на паралелна проекция на обект за дадена проекционна посока зависят само от избора на посоката на проекционната равнина и не зависят от нейното разстояние от обекта. Триъгълник, разположен в равнинатаR1, успоредна на проекционната равнина, се проектира равен на дадената. В този случайab=AB,bc=BC,ac=AC.
В зависимост от ъгъла на наклона на проектиращия лъч към равнината на проекцията, паралелното проектиране се разделя на два вида:правоъгълно и наклонено.
ПРАВОЪГЪЛНА(или ортогонална) проекция се извиква, когато посоката на проекцията е избрана перпендикулярна на равнината на проекцията. В противен случай се наричаКОСА.
При правоъгълна проекция (фиг. 7) стойността на коефициента на изкривяване не може да надвишава единица.
При наклонени проекции (фиг. 5) коефициентът на изкривяване (К=ab/AB) на даден сегментABможе да приема произволни числени стойности в зависимост от наклона на сегмента и проектиращите лъчи към равнината на проекцията. По-специално, ако посоката на сегмента съвпада с посоката на проекцията, тогава проекцията на този сегмент ще бъде точка, а коефициентът на изкривяване е нула.
При паралелна проекция се запазватосновните свойствана перспективата, а именно:
1) проекцията на точка е точка;
2) проекцията на права линия в общия случай ще бъде права линия;
3) всяка точка, принадлежаща на която и да е права, съответства на проекцията на тази точка върху проекцията на тази права.
Също така, паралелна проекцияима редица (само присъщи) свойства:
4) ако една точка лежи на сегмент от права линия, тогава проекцията на тази точка разделя проекцията на сегмента в същото съотношение като
5) проекцията на пресичащите се сегменти ще бъде и пресичащите се сегменти, а точката на тяхното пресичане ще бъде проекцията на пресечната точка на тези сегменти (фиг. 3);
6) проекциите на успоредни сегменти са успоредни, с една и съща посока и съотношението им е равно на отношението на дължините на сегментите, т.е.abcdиAB/CD=ab/cd(фиг. 4);
при правоъгълна проекция прав ъгъл се проектира като прав ъгъл само ако едната му страна е успоредна на проекционната равнина, а другата не е проектиращ лъч(теорема за проекция на прав ъгъл).