Построяване на крива по точки

Метод за линеаризация на данни за y=Ce Ax

Да приемем, че са дадени точки (x1,y1),(x2,y2),…,(xN,yN) и се изисква да се побере експоненциална крива от формата

Първата стъпка е да вземете логаритъм на двете части:

След това променяме променливите:

(единадесет)

В резултат на това получаваме линейна зависимост между новите променливи X и Y:

(12)

Началните точки (xk;yk) на равнината xy са трансформирани в точки (Xk;Y)=(xk;ln(yk)) на равнината XY. Този процес се наричалинеаризация на данните. Тогава линията, конструирана от най-малките квадрати, е корекция на точките k;Yk)>. Нормалните уравнения за намиране на A и B ще бъдат уравненията

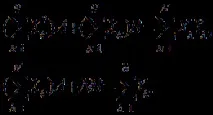
След като A и B бъдат намерени, изчислете параметър C на уравнение (1):

(13)

Пример за изчисление в MATHCAD

Разделяме и получаваме точките Χ и Υ

Решаване на OLS с помощта на вградени функции:

Получаваме резултата с помощта на даден блок:

Практическа задача

Задача: Необходимо е да се напише програма за определяне на гравитационната константа g на следните набори от данни. Използваме нелинейното напасване на най-малките квадрати

Време, т.к	Разстояние, dk
0,200	0,1960
0,400	0,7835
0,600	1,7630
0,800	3,1345
1 000	4,8975

Реализация на метод в MATLAB

z=(C.*exp(0.2*A) -0.1960).^2+(C.*exp(0.4*A)-0.7835).^2+(C.*exp(0.6*A)-1.7630).^2+( C.*exp(0.8*A)-3.1345)+( C.*exp(1.0*A)-4.8975)

Тези. y=0,1271e 3,9115

Внедряване на метода в MATHCAD:

Обяснения:

1) Представете си, че времето и разстоянието са x и y.

2) Ние решаваме най-малките квадрати с помощта на вградени функции.

3) Получаваме резултата с помощта на даден блок. Резултатът е гравитационната константа. които представяме като

Опции за лаборатория

Номер на варианта

функция

Номер на варианта

функция

ТЕМА 2. ЧИСЛЕНО ИНТЕГРИРАНЕ. ПРИБЛИЖИТЕЛНО ИЗЧИСЛЯВАНЕ НА ОПРЕДЕЛЕН ИНТЕГРАЛ

Лаборатория #3

Приблизително изчисляване на определени интеграли»

Целта на работата. Изчислете числено дефиниран интеграл на формата

, където (1)

- a, b - съответно долна, горна граница на интегриране;

- f(x) е непрекъсната функция на отсечката [a, b].

използвайки методите на ляв, десен, среден правоъгълник, трапец и Симпсън.Оценете грешката на резултатите.

Изявление на проблема :

1. Използвайки различни среди за програмиране (MathCad, MATLAB), намерете приблизителната стойност на определения интеграл на функцията f(x) на интервала [a, b] сдаден брой интервали на интегриране n .

2. Приблизителната стойност на интеграла се определя с помощта на методите на левия, десния, средния правоъгълник, трапеца и Симпсън.

3. Оценете грешката при изчисляване на приближения интеграл.

Съдържание на отчета:

1. Постановка на проблема.

2. Теоретична информация.

3. Ръчно изчисляване по формулите на средни правоъгълници, трапеци.

---