Построяване на линия на пресичане на две равнини
Построяване на пресечна линия на две равнини - раздел Философия, Дескриптивна геометрия
Права линия, получена при взаимното пресичане на две равнини, се определя от две точки, всяка от които принадлежи едновременно на двете равнини.
На фиг. 3.37 равнината на общото положение, дадена от триъгълника ABC, пресича фронтално проектираната равнина, дадена от триъгълника DEF, тъй като триъгълникът DEF се проектира върху равнината V под формата на права линия D "F", тогава фронталната проекция на пресечната линия на двете равнини е сегмент K1 "K2". Намираме хоризонталната му проекция и определяме видимостта.
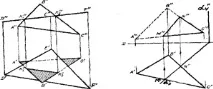
Хоризонтално проектираната равнина a пресича равнината на триъгълника ABC (фиг. 3.3 8).Хоризонталната проекция на пресечната линия на тези равнини е отсечката M'N', която се определя върху следата на оста'.
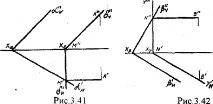
1) намерете точката M' в пресечната точка на следите an' и bn' и точката N" в пресечната точка на an¢ ¢и bn¢¢, а от тях проекциите M" и N'.
2) начертайте прави линии M¢¢N¢¢ и M'N'.
Точките на пресичане на едноименни следи от равнини саследи от линията на пресичане на тези равнини.
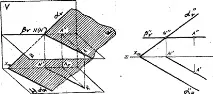
На фигура 3.40 равнините a и b се пресичат. Равнина a е равнина в общо положение, равнина b е хоризонтална равнина. За изгражданее необходима линия на пресичане:
1) намерете точката N" в пресечната точка на следите an¢¢ и bv¢¢;
2) начертайте права линия през тази точка въз основа на позицията
самолети и техните следи.
Фигури (3.40 - 3.42) показват случаи, когато посоката на пресечната линия е известна. Следователно е достатъчно да имате само една точка от пресечната точка на следите и след това да начертаете права линия през тази точка въз основа на позицията на равнините и техните следи.
Тази тема принадлежи към категорията:
дескриптивна геометрия
Кемеровски технологичен институт по хранителна промишленост.. l v Gromov l m Lazareva g m myalenko..
Какво ще правим с получения материал:
Всички теми в този раздел:
Кемерово 2002 UDC:744 (075) Публикувано по решение на Редакционно-издателския съвет на Кемеровския технологичен институт на хранително-вкусовата промишленост Рецензенти: • Доцент, гл.
Успоредна проекция Успоредна проекция на точка ще се нарича пресечната точка на проектираща права, начертана успоредно на дадено направление с проекционната равнина (фиг. 1.2). Паралелни проекции ta
Проекция на точка върху две проекционни равнини Да вземем точка А и да я поставим в пространството на двустенен ъгъл, образуван от две перпендикулярни равнини: фронтална - V и хоризонтална - H (фиг. 1.7).
Проектиране на точка върху три проекционни равнини В случаите, когато две проекции не могат да представят формата на даден обект, той се проектира върху три равнини (Фигура 1.11), т.е. се въвежда равнина на W-профил, тя е перпендикулярна на двете съществуващи, (H
Проекция на отсечка от права 2.1 Проекция на права върху две и три проекционни равнини. Правата линия в пространството се определя напълно от позицията на всеки две точки, принадлежащи натова направо
Взаимно разположение на две линии на комплексния чертеж Ако през дадена точка А е необходимо да се начертае права, успоредна на дадена права LM, тогава конструкцията се свежда до начертаване на права, успоредна на L"M" през точка А и двойка линии през точка А'
Конструиране на отсечка с обща позиция и ъглите на наклона на права линия към проекционните равнини върху чертеж с естествен размер За да определите истинската (естествена) дължина на отсечка от права линия на диаграма, можете да използвате метода на правоъгълен триъгълник (фиг. 2.16, 2.1.7), линия AB - обща позиция (т.е.
Следи на равнина Една равнина може да бъде по-ясно изобразена с помощта на прави линии, по които тя пресича равнините на проекцията. На фиг. 3.6 някаква равнина a е дадена от две пресичащи се прави AB и
Взаимна принадлежност на точка и права равнина. Прави линии със специална позиция От позицията на геометрията следва: 1) права линия принадлежи на равнина, ако минава през две точки, принадлежащи на тази равнина. 2) прав
Положението на равнините спрямо проекционните равнини Възможни са следните положения на равнината спрямо проекционните равнини H,V,W: 1) равнината не е перпендикулярна на нито една от проекционните равнини;
Пресичане на права линия с равнина, перпендикулярна на една или две проекционни равнини Равнина, перпендикулярна на проекционната равнина, се проектира върху последната като права линия. На тази права
Пресичане на права с равнина в общо положение Построяването на пресечната точка на права с равнина в общо положение се извършва по следния алгоритъм: 1) през дадената права (MN) се прекарва някаква помощна равнина (g);
Пресечна точка на две равнини в общо положение Разгледайте общия случай на построяване на правапресичане на две равнини (фиг. 3.47).
Построяване на пресечна линия на две равнини чрез пресечни точки на прави с равнина Този метод се състои в намиране на пресечните точки на две прави, принадлежащи на една от равнините, с друга равнина. Следователно е необходимо да можете да построите пресечната точка на права с
Методи за конвертиране на чертеж Присвояването на прави линии и плоски фигури в определени позиции спрямо проекционните равнини значително опростява конструирането и решаването на проблеми, позволява ви да получите отговор или директно от даден
Въртене около дадена ос Фиг.4.9 Фиг.4.10 Нека точка А се върти около оста i, перпендикулярна на равнината H (Фиг.4.9).
Въртене около избраната ос В някои случаи може да се избере оста на въртене. В този случай, ако оста на въртене е избрана, минаваща през един от краищата на сегмента, тогава конструкцията е опростена, тъй като точката, през която минава оста, ще
Метод на успоредно движение При успоредно движение траекториите на движение на всяка точка от геометричната фигура са в успоредни равнини, а тези равнини (носители на траектория) са успоредни на проекционните равнини
Чертежи на призма и пирамида Ръбовете на призмите и пирамидите са ограничени от ръбове, които са прави сегменти, пресичащи се един с друг. Следователно конструирането на чертежи на призми и пирамиди по същество се свежда до конструиране на проекции
Призми и пирамиди в три проекции, точки на повърхността 5.7 В горните чертежи ребрата са проектирани като сегменти с права линия
Точка и линия върху повърхност По-горе беше казано, че се разглежда повърхносттададено, ако една проекция на точка върху повърхността може да се използва за конструиране
Обща информация за изграждането на линия на взаимно пресичане на две повърхности Линията на пресичане на две повърхности в общия случай е пространствена крива, която може да бъде разделена на две или повече части. Тези части могат по-специално да бъдат извити. Обикновено линии
Пресичане на повърхнини, когато една от тях се проектира Проектиращите повърхнини включват: 1) цилиндър, ако оста му е перпендикулярна на проекционната равнина;
Метод на спомагателни режещи равнини Фигура 5.13 показва, че две извити повърхности A и B се пресичат от трета режеща спомагателна равнина Q. Намерете пресечните линии KL и MN на спомагателната повърхност с всяка от
Пресечна точка на повърхности, описани около една сфера В този случай линиите на пресичане на повърхности от втори ред са две равнинни криви от втори ред
Пресечна точка на пирамидата с равнината Равнината пресича пирамидата в многоъгълник. Ако равнината е успоредна на основата на пирамидата, в разрез се получава фигура, подобна на основата. При изграждане на пресечна линия
Пресичане на призма с равнина При построяване на пресечна линия на призма с равнина се определят точките на пресичане на нейните ръбове с дадената равнина. Тази линия може да бъде конструирана и чрез дефиниране на линиите на пресичане на отделните лица на призмата
Пресичане на конус с равнина В зависимост от посоката на секущата равнина могат да се получат различни линии в участъка на конуса на въртене, наречен връх на конуса, в неговия участък се получава двойка прави линии - образуващи конуса (фиг.
Пресичане на сфера с равнина Всяка равнина пресича сфера в кръг. Ако секателната равнина е успоредна на равнинатапроекции, секционната окръжност се проектира върху тази проекционна равнина без изкривяване. Ако режещата равнина
Пресичане на торус с равнина Криви на Персей При пресичане на торус с равнина могат да се получат различни видове криви линии.
Метрични задачи Метрични задачи се наричат задачи, в които е необходимо да се определят стойностите на измерваните величини - да се измери ъгълът между две прави линии и разстоянието между две точки.
Определяне на реалната стойност на равнинен ъгъл с помощта на неговите ортогонални проекции Решението на задачата се свежда до преместване на равнината с общо положение, към която принадлежи ъгълът, до позиция, успоредна на произволна проекционна равнина. Това движение може да се направи с
Една права е перпендикулярна на равнина, ако е перпендикулярна на две пресичащи се прави, принадлежащи на дадена равнина.
Две равнини са взаимно перпендикулярни, ако една от тях съдържа права, перпендикулярна на другата равнина Следователно построяването на равнина a, перпендикулярна на равнината b, може да се извърши по два начина; 1. Начертаваме права m, перпендикулярна на равнината b (или a), след което ограждаме правата m в равнина
Линеен сегмент се проектира в пълен размер само ако е успореден на равнината, върху която се проектира Във всички останали случаи той се проектира върху равнината на проекцията с изкривяване. За да установите връзката между действителната стойност на сегмент от права линия и неговите проекции, разгледайте ri
Определяне на разстоянието между точка и права. Между две успоредни линии Разстояниеот точка до права линия се определя от стойността на перпендикулярния сегмент, спуснат от точка до права линия: От чертежа (фиг. 7.16) се вижда, че определянето на разстоянието от точка
Разстоянието между равнините се определя от стойността на сегмента на перпендикуляра, пуснат от точка, взета от една равнина в друга равнина Въз основа на дефиницията може да се изпълни алгоритъмът за решаване на задачата за намиране на разстоянието между равнините a и b: 1. Вземете произволна точка A (АОa) в равнината a; 2. От
Методът на нормалните сечения 1. Повърхността се пресича от равнина, перпендикулярна на нейните образуващи (ръбове), фиг. 8.1. Нека разчленим дадената призматична повърхност с фронтално проектираща се равнина Ф, перпендикулярна на ре
Индикатори за изкривяване Съотношенията на аксонометричните координати към естествените (с една и съща естествена единица e) се наричат от магарета индикатори за изкривяване. Означаваме с и индексът на изкривяване в o
Правоъгълна изометрична проекция Образува се, когато координатните оси са еднакво наклонени към картинната равнина P (фиг. 9.1). Оттук и аксономете
Правоъгълна диметрична проекция Най-простата и най-често срещана диметрия се получава, ако u = w и v = Изчислете коефициентите на изкривяване
Наклонени аксонометрични проекции GOST 2.317 - 69 препоръчва използването на наклонена диметрия. В практиката на рисуване най-често се използва такава наклонена диметрия, при която коефициентът на изкривяване по оста y
Има няколко начина да начертаете кръг в изометричния изглед. Първи начин. Построете ромб със страна равна на D на окръжността. Точки А и Б -
Кръг в правоъгълна диметрия В правоъгълна диметрична проекция, точно както в правоъгълна изометрия, малките оси на всичкитри елипси са разположени по посока на тази аксонометрична ос, която отсъства в равнината, копка
Развитие на повърхности, развитие на фасетирани повърхности и повърхности на въртене………………………. 103 8.1. Методът на нормалните сечения. …………. …. 103 8.2. Метод на валцуване ..………………………………………….. 1