Преобразувания на типове сигнали
Формите на математическо представяне на сигнали, особено на етапите на тяхната първична регистрация (откриване) и в директни задачи за описание на геофизични полета и физически процеси, като правило, отразяват тяхната физическа природа. Последното обаче не е задължително и зависи от измервателната техника и техническите средства за откриване, преобразуване, предаване, съхраняване и обработка на сигнали. На различни етапи от процесите на получаване и обработка на информация, както материалното представяне на сигналите в устройствата за запис и обработка, така и формите на тяхното математическо описание по време на анализ на данни могат да бъдат променени чрез подходящи операции за преобразуване на типа на сигналите.
Операцията за дискретизация преобразува аналогови сигнали (функции), които са непрекъснати в аргумента, във функции на моментните стойности на сигналите в дискретния аргумент. Вземането на проби обикновено се извършва с постоянна стъпка в аргумента (равномерно вземане на проби), докато s(t) 10 s(n D t), където стойностите на s(n D t) представляват пробите на функцията s(t) в моменти t = n D t, n = 0, 1, 2. N. Честотата, при която се измерва аналоговият сигнал, се наричачестота на дискретизация. В общия случай решетката за вземане на проби по аргумент може да бъде произволна, като s(t) Yu s(t k ), k=1, 2, ..., K, или да бъде зададена по определен закон. В резултат на семплирането непрекъснат (аналогов) сигнал се преобразува в поредица от числа.
Операцията за възстановяване на аналогов сигнал от неговото дискретно представяне е обратната на операцията по вземане на проби и представлява по същество интерполация на данни.
Дискретизацията на сигналите може да доведе до известна загуба на информация за поведението на сигналите в интервалите между пробите. Все пак има условиядефинирана от теоремата на Котелников-Шанън, според която аналогов сигнал с ограничен честотен спектър може да бъде преобразуван в дискретен сигнал без загуба на информация и след това абсолютно точно възстановен от стойностите на неговите дискретни проби.
Както е известно, всяка непрекъсната функция може да се разложи на краен интервал в ред на Фурие, т.е. представени в спектрална форма - като сума от поредица от синусоиди с множество (номерирани) честоти с определени амплитуди и фази. За относително гладки функции спектърът бързо намалява (коефициентите на модула на спектъра бързо клонят към нула). За представяне на "назъбени" функции, с прекъсвания и "прегъвания", са необходими синусоиди с високи честоти. Казва се, че един сигнал имаограничен спектър, ако след определена честота F всички коефициенти на спектъра са равни на нула, т.е. сигналът се представя като крайна сума от реда на Фурие.
Теоремата на Котелников-Шанън установява, че ако спектърът на сигнала е ограничен от честотата F, тогава след дискретизация на сигнала с честота най-малко 2F е възможно да се възстанови оригиналният непрекъснат сигнал от получения цифров сигнал абсолютно точно. За да направите това, трябва да интерполирате цифровия сигнал "между проби" със специална функция (Kotelnikov-Shannon).
На практика тази теорема е от голямо значение. Например, известно е, че обхватът на аудио сигналите, възприемани от човек, не надвишава 20 kHz. Следователно, когато вземаме проби от записани аудио сигнали с честота от най-малко 40 kHz, можем точно да възстановим оригиналния аналогов сигнал от неговите цифрови проби, което се прави в CD плейърите за възстановяване на звука. Честотата на семплиране на аудио сигнала, записан на CD, е 44100 Hz.
Операцията на квантуване илианалогово-цифрово преобразуване (ADC; английски термин Analog-to-Digital Converter, ADC) се състои в преобразуване на дискретен сигнал s (t n) в цифров сигнал s (n) \u003d s n "s (t n), n \u003d 0, 1, 2. N, като правило, кодиран в двоичната бройна система. Процесът на преобразуване на сигнални проби в числа се нарича квантуване, а произтичащата от това загуба на информация поради закръгляване се нарича грешки при квантуване или шум при квантуване.
Когато преобразувате аналогов сигнал директно в цифров сигнал, операциите по вземане на проби и квантуване се комбинират.
Операцията на цифрово-аналоговото преобразуване (DAC; Digital-to-Analog Converter, DAC) е обратна на операцията на квантуване, докато изходът е или дискретно-аналогов сигнал s(t n), който има стъпаловидна форма (фиг. 1.2.4), или директно аналогов сигнал s(t), който се възстановява от s(t n), например чрез изглаждане.
Тъй като квантуването на сигналите винаги се извършва с определена и неотстранима грешка (максимум - до половината от интервала на квантуване), операциите на АЦП и ЦАП не са взаимно обратни с абсолютна точност.
Псевдоним. Но какво се случва, ако спектърът на аналоговия сигнал е неограничен или има честота, по-висока от честотата на дискретизация?
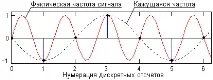
Да предположим, че при запис на акустичен сигнал на оркестър в стая от някакво устройство има ултразвуков сигнал с честота 30 kHz. Записът се извършва със семплиращ сигнал на изхода на микрофона с типична честота 44,1 kHz. При прослушване на такъв запис с помощта на DAC ще чуем шумов сигнал с честота 30 - 44.1/2 » 8 kHz. Реконструираният сигнал ще изглежда така, сякаш честотите са над половинатачестоти на дискретизация, "огледало" от него се отразяваше в долната част на спектъра и се формираше с наличните там хармоници. Това е така нареченият ефектна появата на фалшиви (привидни) честоти(алиасинг). Ефектът е подобен на добре познатия ефект на обратното въртене на автомобилните колела на филмови и телевизионни екрани, когато скоростта на тяхното въртене започва да надвишава честотата на кадрите. Естеството на ефекта може да се види ясно на фиг. 1.2.5. По подобен начин целият високочестотен шум, присъстващ в оригиналния аналогов сигнал, се "отразява" от честотата на дискретизация в основния честотен диапазон на дискретните сигнали.
За да предотвратите псевдонимите, трябва да увеличите честотата на семплиране или да ограничите спектъра на сигнала преди дигитализиране снискочестотни филтри(Нискочестотни филтри,нискочестотни филтри), които пропускат без промяна всички честоти под определената и потискат честотите над определената честота в сигнала. Тази гранична честота се наричагранична честотана филтъра. Честотата на срязване на филтрите против нагласяне е настроена на половината от честотата на дискретизация. Истинските ADC почти винаги имат вграден филтър за антиалиасинг.
Графичното изобразяване на сигналите е добре известно и не изисква специално обяснение. За едномерни сигнали графиката е набор от двойки стойности в правоъгълна координатна система (фиг. 1.2.1 - 1.2.4). При графично показване на дискретни и цифрови сигнали се използва или методът на директните дискретни сегменти на съответната дължина на мащаба над оста на аргумента, или методът на обвивката (гладък или счупен) според стойностите на четене. Поради непрекъснатостта на геофизичните полета и, като правило, вторичния характер на цифровите данни, получени чрез дискретизация и квантуване на аналогови сигнали, вторият метод за графично показванеще се счита за основен.
Тестови сигнали (тестов сигнал). Като тестови сигнали, които се използват при моделиране и изследване на системи за обработка на данни, обикновено се използват сигнали от най-простия тип: хармонични функции синус-косинус, делта функция и функция за скок на единица.
Делта функция или функция на Дирак. По дефиниция делта функцията се описва със следните математически изрази (колективно):
d (t- t) = 0 при t № t,
d(t-t) dt = 1.
Функцията d (t- t) не е диференцируема и има размерност, обратна на размерността на нейния аргумент, което следва директно от безразмерността на резултата от интегрирането. Стойността на делта функцията е нула навсякъде, освен в точката t, където е безкрайно тесен импулс с безкрайно голяма амплитуда, докато областта на импулса е 1.
Делта функцията е полезна математическа абстракция. На практика такива функции не могат да бъдат реализирани с абсолютна точност, тъй като е невъзможно да се реализира стойността, равна на безкрайност в точката t = t на аналоговата времева скала, т.е. определени във времето също с безкрайна точност. Но във всички случаи, когато площта на импулса е равна на 1, продължителността на импулса е доста малка и по време на действието му на входа на която и да е система, сигналът на изхода му практически не се променя (отговорът на системата към импулса е многократно по-голям от продължителността на самия импулс), входният сигнал може да се счита заединична импулсна функциясъс свойствата на делта функция.
Въпреки цялата си абстрактност, делта функцията има добре дефинирано физическо значение. Представете си правоъгълен импулсен сигнал P(t-t) с продължителност q, чиято амплитуда е равна на 1/ q, а съответно площта е равна на 1.Когато стойността на продължителността q намалява, импулсът, намаляващ по продължителност, запазва своята площ, равна на 1, и увеличава амплитудата. Границата на такава операция при q Yu 0 се нарича делта импулс. Този сигнал d (t- t ) се концентрира в една координатна точка t = t, специфичната стойност на амплитудата на сигнала не е дефинирана, но площта (интеграл) остава равна на 1. Това не е моментната стойност на функцията в точката t = t, а именно импулсът (силов импулс в механиката, токов импулс в електротехниката и т.н.) - математически модел на кратко действие, чиято стойност е 1.
Делта функцията имасвойство филтър. Същността му се състои в това, че ако делта функцията d (t-t) е включена в интеграла на която и да е функция като множител, тогава резултатът от интегрирането е равен на стойността на интегранта в точката t от местоположението на делта импулса, т.е.:
f(t) d (t- t) dt = f(t).
Интегрирането в този израз може да бъде ограничено до най-близките околности на точка t.
Функцията за прескачане на единица или функцията на Хевисайд понякога се нарича още функция за включване. Пълен математически израз на функцията:
При моделиране на сигнали и системи стойността на функцията за скок в точката t=0 много често се приема равна на 1, ако това не е от принципно значение.
Функцията за единичен скок се използва за създаване на математически модели на сигнали с ограничена продължителност. При умножаване на произволна функция, включително периодична, с правоъгълен импулс, образуван от две последователни функции на единичен скок
от него се изрязва секция в интервала 0-T, а стойностите на функцията извън този интервал се задават на нула.
Функция на Кронекер. За разделителна способност на дискретни и цифрови системи чрез аргумент на сигналасе определя от неговия интервал на дискретизация D t. Това позволява да се използва дискретен интегрален аналог на делта функцията като единичен импулс - функцията на едно отчитане d (k D t-n D t), което е равно на 1 в координатната точка k \u003d n и нула във всички останали точки. Функцията d (k D t-n D t) може да бъде дефинирана за всякакви стойности на D t = const, но само за целочислени стойности на координатите k и n, тъй като няма други примерни числа в дискретни функции.
Математическите изрази d (t-t) и d (k D t-n D t) се наричат още импулси на Дирак и Кронекер. Въпреки това, използвайки тази терминология, нека не забравяме, че това не са само единични импулси в координатни точки t и n D t, а пълномащабни импулсни функции, които определят както стойностите на импулсите в определени координатни точки, така и нулеви стойности за всички останали координати, в границите от - Ґ до Ґ .