Приложение 1 Бележки към урока Урок № 1 "Числен кръг"

да формират нови знания и да развиват умения по темата „Числова окръжност“;

да насърчава развитието на самоконтрола и речта на учениците;

насърчаване на развитието на когнитивната дейност;

насърчават дисциплината.

повторете единиците за измерване на ъглови стойности;

формулира понятието "Числова окръжност" и дължината на дъгата;

затвърдете придобитите знания на практика.

Тип урок:урок за изучаване на нов материал.

Организационен момент - (2 мин.);

Актуализиране на опорни знания - (7 мин.);

Учене на нов материал - (18 мин.);

Затвърдяване на изучения материал - (13 мин.);

Резултатът от урока - (3 мин.);

Домашна работа - (2 мин.).

1. Организационен момент.

-съобщение на темата на урока;

- поставяне на целта на урока.

2. Актуализиране на опорни знания.

проверете степента на усвояване на предварително изучен материал;

за актуализиране на знанията на учениците, необходими при изучаване на нова тема.

- Да си припомним градусните и радианните мерки на ъглите от курса по геометрия (слайд 4).

Преобразувайте следните ъгли от градуси в радиани: 1 0 , 180 0 , 45 0 , 60 0 (слайд 4).

(Първо, заедно с учениците, описваме подробно как се преобразува от градус в радианова мярка, след това те изпълняват самостоятелно по двойки и след това проверяваме правилността на задачата).

Намерете мярката в радиан на неизвестния ъгъл. Намерете градусната мярка на всички ъгли на триъгълника (слайд 5).

Намерете радианната мярка на ъглите на триъгълник, ако техните стойности са свързани като 2: 3: 4 (слайд 6)

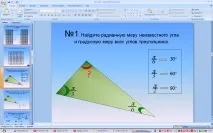
- Неизвестният ъгъл е

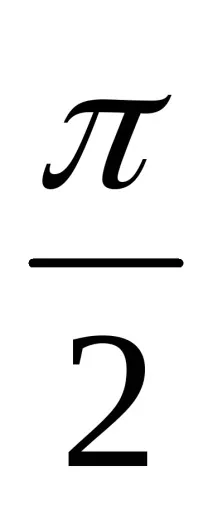
- Сумата от ъглите на триъгълник е 180 0 или

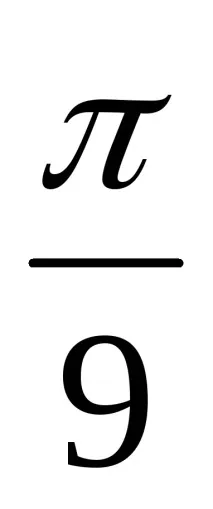
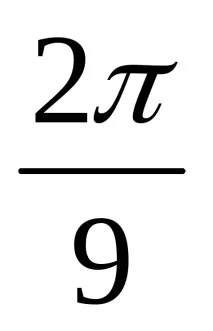
, тогава 2x + 3x + 4x =

, 9x=

, следователно x =

, тогава 2x =

3x =

и 4x =

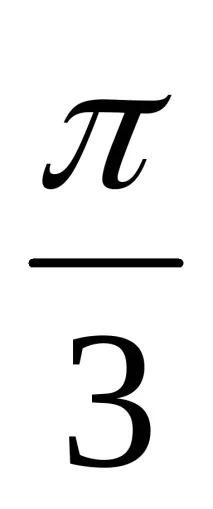
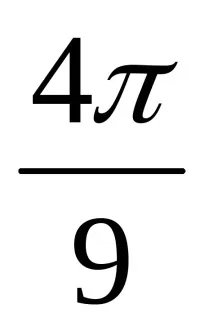
Изучаване на нов материал.

да се формулира понятието "Числова окръжност".

- Още не сте се срещали с числовия кръг, но сте добре запознати с числовата ос. Можете ли да ми кажете какво е числова ос?

- Точно така, това е права линия, на която са зададени началната точка О, мащабът (отсечка) и положителната посока (слайд 7).

На числовата ос можем да се движим както в положителна, така и в отрицателна посока.

- Така че числовата окръжност има начална точка О, мащабът. На него също са отбелязани точки, както в положителна посока, обратно на часовниковата стрелка, така и в отрицателна посока, по часовниковата стрелка (слайд 8).

- Цифровият кръг е разделен на 4 четвърти (слайд 8). Обиколката, както знаем, е C=2

R. За удобство ще обозначим нашия радиус равен на 1, т.е. ще разгледаме единичната окръжност С=2

(слайд 8).

- Както казах, върху тази окръжност с номер на единица можем да маркираме точки. Нека начертаем кръг. Маркираме началната точка O и ще маркираме точките, както в положителна, така и в отрицателна посока. Да започнем със следните точки

, (слайд 9)

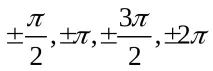
- Начертайте друг кръг и маркирайте следните точки

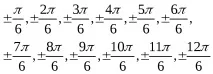
- Освен това точките са разположени симетрично една спрямо друга (слайд 10).

- Когато маркирахме тези точки върху числовия кръг, какво забеляза?

- Браво, нали. Начертайте друг кръг и маркирайте следните точки

, (слайд 11)

- Много добре. Нека начертаем още една окръжност и маркираме следните точки, (слайд 12)

- Много добре. Сега ще приложим всички тези стойности къмедин кръг с числа(Учениците поставят стойности в един кръг), (слайд 14).

- това е права линия, на която са дадени началната точка O, мащабът (единичен сегмент) и положителната посока.

На числовата ос можем да се движим както в положителна, така и в отрицателна посока.

(учениците рисуват кръг и отбелязват върху него всичко, което е показано на слайда)

(учениците рисуват кръг в тетрадките си).

(Учениците отбелязват тези точки и със знак минус ги отбелязват сами)

(Учениците отбелязват тези точки и със знак минус ги отбелязват сами).

- забелязахме, че

съвпада с

съвпада с 2

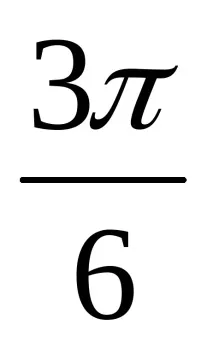
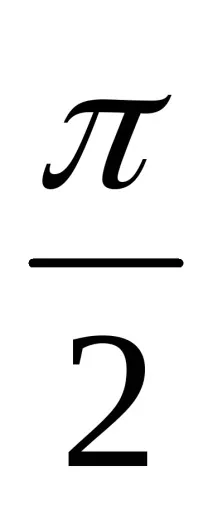
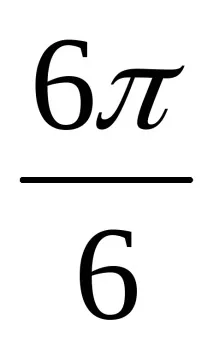
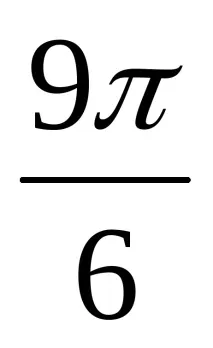
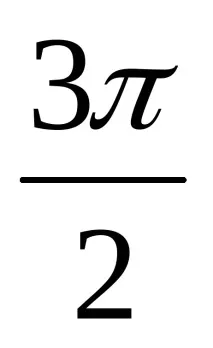
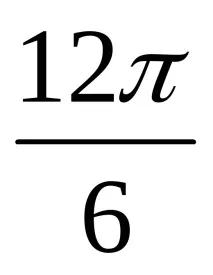
(Учениците отбелязват тези точки. Учениците също заместват, че някои стойности са еднакви),

(Учениците поставят стойности в едно числово кръгче)

Затвърдяване на изучения материал.

да формират умение за решаване на примери за прилагане на нови

- Намерете точките от числовата окръжност, които отговарят на даденото число

- Втората четвърт от единичната окръжност е разделена наполовина от точката М, а четвъртата е разделена на 3 равни части от точките К и Р. Какви са дължините на дъгите AM, AK, AP?

- Намерете всички числа t, които върху числовата окръжност съответстват на точките, принадлежащи на дъгите a) AB, b) DB, c) BD

- По буква а) ще решим заедно с мен

- Arc AB е дъга с начало в точка A и край в точка B при движение по окръжност обратно на часовниковата стрелка, така че t = 0 и t =

. Така че за точка t от дъгата AB имаме:

. Както видяхмепо-рано точка А съответства не само на числото 0, но и на всички числа 0 +2
k,т.е. 2

k, т.е. B съответства на

. Така че

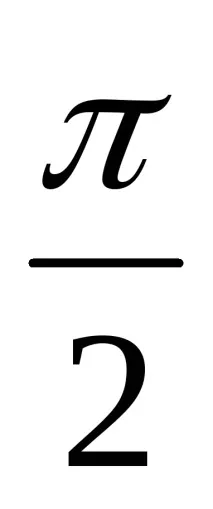
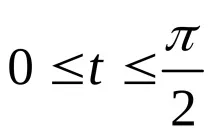
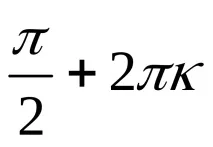
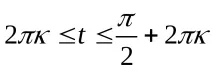
- По букви б) и в) самостоятелно, а след това ще проверим дали сте решили правилно.

- Сега се разделете на групи от по 4 души и направете тест по разгледаната тема.

(Учениците използват маркер, за да маркират тези точки върху кръга на интерактивната дъска)

AM = AB + VM =

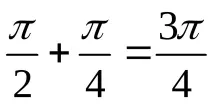
AK \u003d AD + DK \u003d

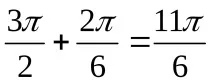
AP = AD + DA =

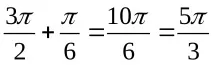
(Учениците заедно с учителя записват решението на задачата)