Приложение за сплайн инструмент
Грешка при интерполация чрез кубични сплайни
Нека ни е дадена някаква функцияƒ(x), дефинирана в интервала [a,b], и дадена нарастваща последователност от интерполационни възли
По дефиниция кубичният сплайн е непрекъсната полиномиална функция на части (съставена от полиноми от трета степен), която има непрекъснати първа и втора производни в интерполационните възли.
Основният кубичен сплайн, интерполиращ функциятаƒ(x)в тези точки, е кубичният сплайнs(x), така че:
- тя съвпада с интерполираната функция в интерполационните възли, т.е.s(xk) = ƒ(xk)за всичкиk = 1,2. n6;
- и са изпълнени следните гранични условия
задаването на гранични условия е необходимо за недвусмисленото определяне на коефициентите на кубичните полиноми, които изграждат сплайна.
Ще се интересуваме от поведението на максималното отклонение на сплайн от интерполираната функция в зависимост от максималното разстояние между съседни интерполационни възли, т.е. величина зависимост
от стъпкаh, където , както и колко добре производните на сплайна приближават производните на интерполираната функция.
Грешка при интерполация на функция
Известно е, че ако функциятаƒ(x)има четири непрекъснати производни, тогава следната оценка е вярна за интерполационната грешка от основния сплайнs(x)
и константата в това неравенство е най-добрата възможна.
За да демонстрираме това твърдение, нека интерполираме, например, функциятаƒ(x)= sinxвърху сегмента [0.3π/2] чрез основен кубичен сплайн по равномерно разположени възли, намалявайки разстоянието между съседни възли и наблюдавайки поведениетоинтерполационни грешки.
За да изградим фундаментален кубичен сплайн, ние използваме функцията csape, която е част от Spline Toolbox. Тази функция ви позволява да конструирате кубичен сплайн с произволни гранични условия. В нашия случай граничните условия са:
Функцията csape приема три входни аргумента:
- вектор с абсцисите на интерполационните възли;
- вектор, чийто първи елемент е стойността на производната на сплайн на лявата граница на сегмента, следващите елементи са стойностите на интерполираната функция във възлите, а последният елемент е стойността на производната на сплайн на лявата граница на сегмента;
- вектор от две числа - порядъци от производни, за които са посочени стойности, в нашия пример, производни от първи ред, следователно трябва да се посочи векторът [1, 1].
Функцията csape връща сплайн в частична полиномиална форма като структура, чиито полета съдържат коефициенти, възли, ред (вижте раздел „Интерполация чрез кубични сплайни, функция csape“). Можете да работите с тази структура допълнително, като извършвате различни сплайн операции, като използвате функциите на Spline Toolbox.
За да изчислим стойността на сплайн в дадени точки, използваме функцията fnval, чиито входни аргументи трябва да бъдат структура с информация за сплайн и вектор от стойности на независимата променлива. Функцията fnval връща стойностите на кубичния сплайн, изчислени в тези точки.
Ще променим разстояниетоhмежду интерполационните възли в цикъла, като приемем на всякаk-та стъпка от цикълаh = 2 kи ще натрупаме стойностите на стъпката и съответните стойности на грешката на интерполация в масивите H и Err.
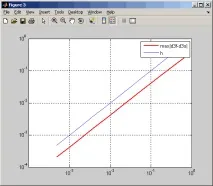
На графиката по абсцисната ос нанасяме стойността на стъпката между възлите, а по ординатната ос стойността на интерполационната грешка, която ще изчислим катомаксималното отклонение, установено от достатъчно голям набор от междинни точки между интерполационните възли (ние ги вземаме 30 пъти повече от интерполационните възли). За по-голяма яснота ще покажем и дясната страна на оценката на графиката, в която ще я заменим с 1, т.к. максималната стойност на модулите на производните на функцията sinxне надвишава 1.
По-долу е текстът на съответния m-файл SplineErr.m
След изпълнение на този m-файл получаваме графика със зависимостта на интерполационната грешка и нейната оценка, от която се вижда, че интерполационната грешка от кубичния фундаментален сплайн има редh 4и не надвишава оценката на грешката.
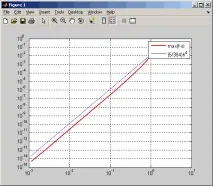
Обърнете внимание, че съществена роля играе фактът, че стойностите на първите производни на сплайн в граничните точки на интерполационния сегмент съвпадат със стойностите на първите производни на интерполираната функция. Ако изградите сплайн, за който например първата производна в дясната точка на сегмента ще бъде равна не на 0, а на 1, тогава степента на конвергенция значително намалява и става от порядъка наh. За да демонстрираме този факт, достатъчно е да присвоим стойност 1 на променливата dfb в m-файла SplineErr.m.Тогава получаваме следното поведение на грешката при интерполация на кубичен сплайн.
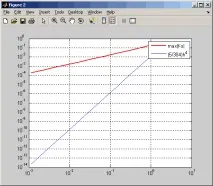
Гладкостта на интерполираната функция също значително влияе върху скоростта на намаляване на грешката по време на интерполация чрез основни кубични сплайни. Да разгледаме например интерполацията на функциятаx 2 xвърху сегмента [-1;1]. При нула тази функция има прекъсната трета производна.
За да интерполирате тази функция чрез фундаментални сплайнове, достатъчно е във файла SplineErr.mзаменете първите пет реда със следните
(стойностите на първите производни на функциятаx 2 xв граничните точки на интерполационния сегмент са равни на -3 и 3). В резултат на това получаваме графика, от която може да се види, че скоростта на конвергенция на интерполационната грешка е от порядъка наh 3.
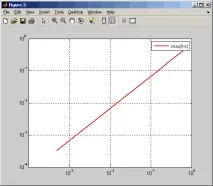
По-нататъшното намаляване на гладкостта на интерполираната функция ще доведе до намаляване на скоростта на намаляване на интерполационната грешка, например, когато интерполираме функциятаxx(чиято втора производна е прекъсната в точка 0) върху сегмента [-1;1] чрез кубичен фундаментален сплайн, получаваме следния резултат.
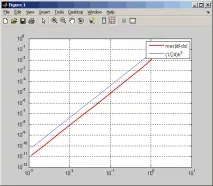
Кубичните сплайни осигуряват добра апроксимация на производните на интерполираната функция. Нека дадем оценки за апроксимационната грешка на производните на четири пъти непрекъснато диференцируемата функцияƒ(x), когато тя е интерполирана от основния кубичен сплайнs(x).
Както следва от оценката по-долу, апроксимацията на първата производна води до грешка от порядъкаh 3.
и константата в това неравенство е най-добрата възможна.
За да демонстрирате това твърдение, можете да използвате m-файла DerErr.m, чийто текст е даден по-долу. M-файлът DerErr.m дефинира вградени функции за изчисляване на интерполираната функция и нейната първа производна. По-нататък в цикъла стъпката между равномерните интерполационни възли намалява и за всяка стойност на стъпка се намира максималното отклонение на производната на основния кубичен сплайн от производната на интерполираната функция по отношение на 30 междинни точкимежду съседни възли. За да се конструира основен кубичен сплайн, както в примера SplineErr.m, се използва функцията csape, а производната на сплайн се намира с помощта на функцията fnder, включена в Spline Toolbox, която връща сплайн, съставен от квадратни полиноми.
В резултат на това получаваме графика, от която може да се види, че конвергенцията е от порядъка наh 3, както установява теоретичната оценка.
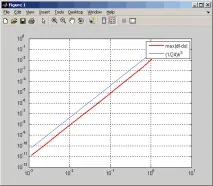
Следната оценка показва, че максималното отклонение на производната на функцията и производната на основния кубичен сплайн в интерполационните възли намалява с порядък по-бързо от тяхното максимално отклонение за целия интервал
За да демонстрирате това твърдение, можете леко да промените m-файла DerErr.m, като изчислите в него само максималното отклонение във възлите
Разбира се, за да получите график за оценка, трябва да пишете
и съответно променете легендата.
След като направихме тези промени, получаваме графика на поведението на грешката на приближаване на първата производна в интерполационните възли (намаляването на скоростта на конвергенция, когато стъпката се доближава до 10 -3, се дължи на грешки при закръгляване).
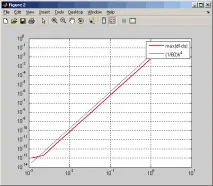
При апроксимиране на второто производно скоростта на сближаване е с порядък по-ниска, отколкото при апроксимиране на първото производно, а съответната оценка на грешката на апроксимацията има формата
За да демонстрирате това твърдение, е достатъчно да промените малко m-файла DerErr.m. В началото добавете вградена функция, за да зададете втората производна на интерполираната функция
Заза да изчислите второто производно на сплайн, можете отново да използвате fnder, като го извикате с втори входен аргумент от 2 (реда на производното)
За да намерим максималното отклонение, използваме
Съответно с оценката трябва да се промени графикът му.
В резултат на това получаваме
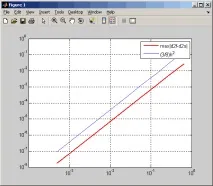
За третата производна в случай на равноотдалечени интерполационни възли е валидна следната оценка
което е лесно да се демонстрира чрез извършване на подходящи промени в m-файла DerErr.m. Получаваме следната графика