Процесът на смърт и размножаване - Студопедия
Нека разгледаме още една типична схема на непрекъснати вериги на Марков - така наречената схема на смъртта и размножаването, която често се среща в различни практически задачи.
Марков процес с дискретни състоянияS0, S1, . Snсе нарича процессмърт и възпроизвеждане, ако всички състояния могат да бъдат изтеглени в една верига, в която всяко от средните състояния (S1, S2, . Sn-1) може да отиде само в съседни състояния, които от своя страна се връщат назад, а крайните състояния (S0 и Sn) отиват само в съседни състояния (фиг. 3.7). ).
Името е взето от биологични проблеми, където състоянието на популациятаSkозначава наличието наkединици индивиди в нея.
Преходът надясно се свързва с размножаването на единици, а наляво - с тяхната смърт.
Ориз. 3.7. Графика на състоянието за процеса на смърт и размножаване
lиμимат индекса на състоянието, от което излиза стрелката.
Неслучайна променливаXkе свързана със състояниетоSk: ако систематаSе в състояниеSkв моментt, тогава дискретната случайна променливаX(t), свързана с работата на системата, приема стойносттаk. Така получаваме случаен процесХ(t),, който рязко променя състоянието си в произволни, предварително неизвестни моменти от време.
Процес на Марковна смърт и възпроизвеждане с непрекъснато времее случаен процес, който може да приема само неотрицателни цели числа. Промените в този процес могат да настъпят по всяко време, т.е. по всяко време той може или да се увеличи с единица, или да намалее с единица, или да остане непроменен.
В практиката има процеси на чисторазмножаване и чиста смърт. Процесът на чисто възпроизвеждане е такъв процес на смърт и размножаване, при който интензитетите на всички смъртни потоци са равни на нула; по същия начин, процесът на чиста „смърт“ е такъв процес на смърт и възпроизводство, при който интензитетите на всички възпроизводствени потоци са равни на нула.
Пример 1. Нека разгледаме работата на модели автомобили от една и съща марка в голяма транспортна компания (в предприятие). Интензивността на пристигането на автомобили в предприятието е равна наl(t). Всяка кола, получена от предприятието, се отписва след случайно времеTc. Срокът на експлоатация на автомобилаtсе разпределя по експоненциалния закон с параметъраm. Процесът на работа на автомобила е случаен процес.A(t)- броят на автомобилите от тази марка, които са в експлоатация в моментаt. Нека намерим едномерния закон на разпределение на случайния процесPi(t) = P,ако: 1) няма ограничения за броя на управляваните автомобили, 2) не повече отnавтомобили могат да се експлоатират в предприятието.
1. Случаен процес на работа на автомобила е процес на смърт и размножаване, чиято обозначена графика е показана на фиг. 3.8.
Ориз. 3.8. Графика на състоянието
Системата от уравнения на Колмогоров, съответстваща на тази графика, има формата
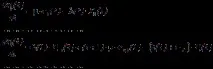
Ако в началния момент от времеt= 0 в предприятието нямаше нито една кола, тогава тази система от уравнения трябва да бъде решена при началните условияP0(0)= 1,Pi(0)= 0 (i= 1, 2, …). Ако приt= 0 предприятието е ималоkколи (k= 1, 2, .), тогава първоначалните условия ще изглеждат така
2. Ако предприятието може да управлява не повече от n автомобила от модели от една и съща марка, тогава има процес на смърт и възпроизводство с ограничениброя на състоянията, чиято обозначена графика е показана на фиг. 3.9.
Ориз. 3.9. Графика на състоянието
Системата от уравнения на Колмогоров за обозначена графика (фиг. 3.9) има формата (3.4).
Тази система трябва да бъде решена при началните условия, обсъдени по-горе. Решенията на системите от уравнения (3.4) и (3.5) са едномерни закони на разпределениеРi(t).Намирането на решения на системи в общ вид за произволен вид на функциятаl(t)представлява значителни трудности и няма практическо приложение.

При постоянни интензитети на потоци на смърт и размножаване и краен брой състояния ще съществува стационарен режим. СистематаSс краен брой състояния (n+ 1), в която процесът на смърт и възпроизводство протича с постоянни интензитети на потоците на смъртта и възпроизводството, е най-простата ергодична система. Означената графика на състоянието за такава система е показана на фиг. 3.9.
Граничните (окончателни) вероятности на състояния за най-простия ергодичен процес на смърт и размножаване, който е в стационарен режим, се определят по следните формули:
(3.6)
(3,7)
Правило. Вероятността заk-то състояние в схемата на смъртта и размножаването е равна на дроб, чийто числител е произведението на всички интензитети на възпроизвеждане вляво отSk, а знаменателят е произведението на всички интензитети на смърт вляво отSk, умножено по вероятността от лявото състояние на крана на систематаP0.
В предишния пример за стационарен режим, ако интензивността на пристигащите автомобили е постоянна (l(t) = l = const), тогава вероятностите за крайно състояние, при условие че няма ограничения за броя на автомобилите в предприятието, са
(3,8)
. (3,9)
ПриВ този случай математическото очакване на броя на управляваните автомобили е равно на неговата дисперсия:
Ако има ограничение за броя на автомобилите в предприятието (не повече отn), тогава крайните вероятности могат да бъдат записани, както следва:
(3.11)
(3.12)
Математическо очакване на броя на управляваните автомобили в стационарен режим
(3.13)
Пример 2. Производствената линия включва четири машини. Екип от четирима обслужващи служители извършва профилактика на всяка от тях. Общият поток от моменти на завършване на ремонта за целия екип е Поасон с интензитетl(t).След завършване на ремонта машината се проверява; с вероятностРсе оказва ефективен (времето за проверка е кратко и може да бъде пренебрегнато в сравнение с времето за профилактика). Ако машината се окаже неработоспособна, тогава отново се извършва нейната профилактика (времето за която не зависи от това дали е била извършена по-рано) и т.н. В началния момент всички машини се нуждаят от профилактика. Задължително:
1. Постройте графика на състоянието за систематаS(четири машини).
2. Напишете диференциални уравнения за вероятности за състояния.
3. Намерете математическото очакване на броя на машинитеMt, които са преминали успешно профилактика до моментаt.
Графиката на състоянието е показана на фиг. 3.10, в който:
S0 –и четирите машини се нуждаят от превантивна поддръжка;
S1– една машина е преминала успешно профилактика, а три имат нужда от профилактика;
S2– две машини са преминали успешно профилактика, а две имат нужда от профилактика;
S3– три машини са преминали успешно профилактика, една има нужда от профилактика;
S4- и четиритемашината е преминала успешно превантивната поддръжка.
Ориз. 3.10. Графика на състоянието на системата
Всяка превантивна поддръжка е успешно завършена с вероятностP, което е еквивалентно наP-преобразуване на потока от ремонтни завършвания, след което ще остане поасонов, но с интензитетPl(t). В този пример имаме работа с чист процес на умножение с ограничен брой състояния.
Уравненията на Колмогоров имат следния вид:
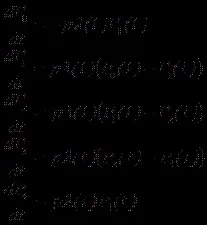
Начални условияP0(0)= 1,P1(0)= … =P4(0)= 0. При постоянен интензитетl(t) = lи вероятностите за състояние се определят по следните формули:
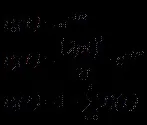
Математическото очакване на броя на дисковете, преминали успешно превантивна поддръжка към момента t е равно на
Пример 3. Да разгледаме производството на автомобили във фабрика. Потокът от произведени автомобили е нестационарен по Поасон с интензитетl(t).Да намерим едномерния закон за разпределение на случайния процесX(t)- броят автомобили, произведени до времевата точкаt, ако в моментаt= 0 е започнало производството на автомобили.
Очевидно е, че тук процесът на чисто възпроизвеждане е без ограничение на броя на състоянията, докатоli(t) = l(t), тъй като интензивността на производството на автомобили не зависи от това колко коли вече са произведени. Графиката на състоянието на такъв процес е показана на фиг. 3.11.
Ориз. 3.11. Графика на състоянието
Едномерният закон на разпределение на случайния процесX(t)за графиката, показана на фиг. 3.11 се определя от следната система от уравнения на Колмогоров:

Тъй като броят на освободените колиX(t)във всеки фиксиран моментtсе разпределя съгласно закона на Поасон с параметъра
ПроцесътX(t), разглеждан в този пример, се наричанехомогенен процесПоасон.Ако интензитетl(t) = l = const, тогава получавамехомогенен процес на Поасон. За такъв процес сP0(0)= 1,Pi(0) = 0 (i > 0)
Характеристиките на процеса на Поасон ще бъдат
Задача 1. Има устройство, което се състои от четири възела; потокът от откази е най-простият, средното време на безотказна работа на всеки възел е 11 часа. Неуспешният възел веднага започва да се ремонтира; Средното време за ремонт на възел е 2 часа. (потокът за възстановяване е най-простият). Намерете средната производителност на устройството, ако с четири работещи възли е 100%, с три 60%, с две или по-малко устройството изобщо не работи.
Не намерихте това, което търсихте? Използвайте търсачката:
Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо