Просто изчисление на рекурсивен филтър от 1-ви ред
Има проби (данни) на входа на нашия филтър, нека това е последователността X. Има проби от изхода на филтъра, нека това е последователността Y. Филтърът изпълнява следната обработка:
Y(n) = Alfa*Y(n-1) + Beta*X(n) Тоест следващата проба Y(n) се получава чрез претеглено събиране на предишната изходна проба и новия входен код (от ADC, например). В този случай обикновено е желателно коефициентът на усилване на филтъра да бъде равен на 1. За да направите това, е необходимо
Алфа + Бета = 1
В рамките на тази бележка задачата за изчисляване на цифров рекурсивен филтър от 1-ви ред е да се намерят коефициентитеAlfa иBeta, като се вземе предвид удобството на тяхното използване в микроконтролер (MC) за цифрово филтриране на проби.
СОФТУЕРНО РЕАЛИЗИРАНЕ
Ако работим с MK, тогава е много добра практика да използваме целочислена аритметика. Дори работата с 32-битови LONG променливи в 8-битов MCU е много по-бърза тук, отколкото с FLOAT. Така че изберетеAlfa иBeta по този начин:
Alfa = Na Beta = Nb Na + Nb = 2^k С други думи, вместо дробниAlfa иBeta се вземат цели числа и дори така, че сумата им да е равна на цяла степен на две: 2, 4, 8, 16, 32, 64, 128, 256, 51 2 и др. Тогава процесорът има по-малко работа:
Y(n) = (Na*Y(n-1) + Nb*X(n)) >> k4
Умножете 2 пъти цяло число по цяло число, добавете, преместете надясно сk цифри. Това е всичко за внедряването на софтуера. Как да изчислим филтъра, т.е. намерете правилнитеNa иNb ?
ИЗЧИСЛЕНИЕ НА ФИЛТЪРА
В нашия случай можем да преминем от необходимите честотни свойства или от времето на преходния процес. Мисля, че по-често вграждащият се задава точно от времененпараметри. Нека разгледаме този случай. Да приемем, че дизайнерът знае колко бързо трябва филтърът да обработи промяна във входния сигнал. Как нашият филтър обработва такъв сигнал? Ако дадем скок от нула до някаква стойност, обозначена като 100%, тогава ще видим нещо подобно на изхода на филтъра:
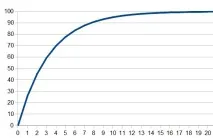
Както можете да видите, на 8-ия брой филтърът вече е отработил 90% от входното действие, на 10-ия - 95% и т.н. Прието е да се говори за "недовършени", т.е. за тези 10 или 5 процента, с които филтърът все още „лъже“ към някакъв вид обратно броене. Те също така казват, чегрешката при настройката на изходния сигнал е толкова много процента. След това давам формули за грешката на установяване от 5 до 0,1%. В първия случай преходният процес е приключил "на око", а точност от 0,1% обикновено е достатъчна, за да се счита, че процесът е напълно завършен. Разликата между тези 5% и 0,1% филтри не е толкова голяма. Изчислете и запазете две константи, ограничаващи числотоNtau
LN(1/5%) = 2,996 LN(1/0,1%) = 6,908 Ntau = 2,996. 6,908 Тези рамки скоро ще ви бъдат полезни. Да не забравяме, че долната граница отговаря на "грубия" процес, когато бързаме да считаме разработката за завършена, а горната - на "точния" преходен процес.
И така, разработчикът зададе времето на преходния процесTpp, през който филтърът ще завърши скока с 95.99.9%. Какво още трябва да знаете? Времето за вземане на проби е периодът, с който пробите пристигат на входа на филтъра и резултатите напускат филтъра със същата скорост. Нека просто го наречемT. Ясно е, че много показания ще бъдат обработени по време на преходния процес. Колко?
N = Tpp / T И нашата задача е да изберем стойноститеNa,Nb иk, така че да се поберат вTpp. Оказва се, че всичкимного просто. Трябва да е изпълнено условието:
Алфа > 8
Ако не се стремите към конкретна цифра на грешката при установяване, тогава можете да опитате да изхвърлите едно умножение, като изберете по-малкото от числатаNa иNb равно на 1. Погледнете реда на таблицата "1/Бета". Стойностите1/Beta са между 14 и 33. Това означава, че мога да избера2^k като 16 или 32:
Y(n) = (31*Y(n-1) + X(n)) >> 5
Y(n) = (15*Y(n-1) + X(n)) >> 4
В първия случай сме близо до "груб" процес, за нашите 100 проби ще получим около 95% от стойността в стационарно състояние. Във втория случай влиянието на показанията X е много по-силно и в същото време почти ще влезем в зоната на 99,9%. Има по-малко възможности за избор за втората колона. Единствената стойност2^k, която може да бъде избрана, е 2.
Y(n) = (1*Y(n-1) + 1*X(n)) >> 1
и получаваме "точен" филтър. Ако изберете2^k = 4, то при 10 проби процесът няма да влезе в 95% (а ще влезе малко по-късно). Третата колона също предлага една проста опция:
Y(n) = (255*Y(n-1) + 1*X(n)) >> 8
В този случай ние прилагаме "среден" филтър, грешката на настройката е между 0,1 и 5%.
Колона 1 изисква да работите с по-малкия от коефициентите - и сега това еAlfa. След като дефинирахме диапазона от стойности1/Alfa = 20.1000, можем лесно да приложим филтър, близък до „груб“:
Y(n) = (Y(n-1) + 31*X(n)) >> 5
или близо до точно:
Y(n) = (Y(n-1) + 511*X(n)) >> 9
или дори по-точно от "точно" :)
Y(n) = (Y(n-1) + 1023*X(n)) >> 10
И така, приключихме с примерите.
ОБОБЩЕНИЕ
Първо. Нека зададем времето на преходния процес, периода на пробите и да изчислим колкопроцесът на извличане трябва да приключи:
N = Tpp / T
Второ. Нека изчислим границите на коефициента при Y
Алфа > k4
Както е показано в примерите, понякогаNa илиNb могат да бъдат зададени равни на 1, което опростява изчисленията.