Проучванесиметричен вибратор, стр. 4

За вибратор, чийто диаметър е много по-малък от дължината му, в първото приближение може да се приеме, че амплитудата на тока по дължината му се променя по синусоидален закон в случай на хармоничен сигнал. Във вибратора, както и в дълга линия, отворена в края, се установява режимът на стояща вълна, а възелът на тока (антинод на напрежението) винаги се намира в краищата на вибратора. На фиг. 4.3, 4.4 показва диаграми на разпределение на тока и напрежението по протежение на вибратора с дължина на рамото , ℓ = 0.75l, ℓ = λ.

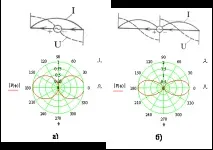Фигура 4.3 - Диаграми на ток и напрежение и модели на излъчване на симетричен вибратор с дължина на рамото:

а) l = 0,25λ, б) l = 0,5λ

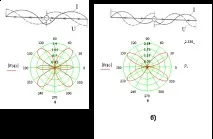
Фигура 4.4. – Диаграми на ток и напрежение и диаграми на излъчване на симетричен вибратор с дължина на рамото:

а) l = 0,75λ, б) l = λ

Външният проблем също има строго решение, базирано на системата от вълнови уравнения, като се вземат предвид граничните условия. Проблемът обаче значително се опростява, ако се използва методът на геометричната оптика. В съответствие с този метод симетричен вибратор с крайна дължина може да бъде представен от набор от елементарни електрически радиатори, които образуват линейна антенна решетка. Полученото поле в произволна точка в пространството е геометричната сума от полетата на отделните елементи на решетката. Това се разбира като добавяне на полетата на отделните източници, като се вземат предвид техните амплитуди и фази: .

Като се има предвид, че броят на елементите в решетката е безкраен, операцията на добавяне се заменя с интегриране по дължината на вибратора: . Пропускайки междинните математически операции, даваме крайната формула за силата на електрическото поле, създадено от симетричен вибратор:

(4.1)

където: k – вълново число;

Ip е амплитудата на тока в антинода;

ℓ - дължина на рамото на вибратора;

j - текущ ъгъл.

Първият фактор определя фазата на полученото поле, вторият - неговата амплитуда, третият - зависимостта на амплитудата на полето от ъгъла на байпаса на вибратора по окръжност с произволен радиус r.

Последният множител се нарича модел на посоката на симетричния вибратор:

(4.2)

Насочените модели в полярни или декартови координати обикновено се изграждат в нормализирана форма, т.е. начертайте текущите стойности на F(j), разделени на максималната стойност на графиката. В противен случай диаграмите, изградени на различни нива на полета, не могат да бъдат сравнени.

Както следва от формула (4.2), формата на диаграмата на излъчване зависи от електрическата дължина на вибратора. Наличието във формула (4.2) на периодичните функции sin и cos е причината в общия случай диаграмата на излъчване да има редица максимуми и минимуми. Секциите на диаграмата между два съседни минимума се наричат лобове. При j = 0 се осъществява максимумът на главния лоб. Останалите максимуми съответстват на вторични или странични лобове.

С увеличаването на съотношението ширината на главния лоб и нивото му намаляват, а при започва да се появява първият страничен лоб. Когато нивото на страничния лоб стане по-високо от нивото на главния лоб и когато главният лоб изчезне напълно (фиг. 4.3, 4.4). Ширината на главния лоб на диаграмата на излъчване се определя или от нулево излъчване - j0, или от половин мощност - j0,5 (фиг. 4.5).

AltGTU 419
AltGU 113
AMPGU 296
ASTU 266
BITTU 794
BSTU "Voenmekh" 1191
BSMU 172
BSTU 602
BSU 153
БСУИР391
БелГУТ 4908
BSEU 962
БНТУ 1070
BTEU PK 689
БрСУ 179
ВНТУ 119
VGUES 426
ВлГУ 645
VMEDA 611
ВолгГТУ 235
ВНУ им. Далия 166
VZFEI 245
ВятГША 101
ВятГГУ 139
ВятГУ 559
GGDSK 171
GomGMK 501
GSMU 1967
GSTU im. Сухой 4467
ГСУ им. Скарина 1590г
GMA им. Макарова 300
ГДПУ 159
DalGAU 279
DVGGU 134
DVGMU 409
DVGTU 936
DVGUPS 305
FEFU 949
ДонГТУ 497
DITM MNTU 109
IVGMA 488
IGHTU 130
ИжГТУ 143
KemGPPC 171
KemGU 507
KSMTU 269
Киров АТ 147
KGKSEP 407
KGTA им. Дегтярев 174
КнАГТУ 2909
КрасГАУ 370
КрасГМУ 630
KSPU им. Астафиева 133
KSTU (SFU) 567
КГТЕИ (СФУ) 112
PDA № 2 177
КубГТУ 139
КубСУ 107
KuzGPA 182
КузГТУ 789
MSTU им. Носова 367
МГУ ги. Сахарова 232
IPEC 249
МГПУ 165
МАИ 144
МАДИ 151
MGIU 1179
MGOU 121
MGSU 330
Московски държавен университет 273
МГУКИ 101
MGUPI 225
MGUPS (MIIT) 636
МГУТУ 122
MTUCI 179
ХАЙ 656
TPU 454
NRU MPEI 641
НМСУ "Горни" 1701
ХПИ 1534
НТУУ "КПИ" 212
НУК тях. Макарова 542
HB 777
NGAVT 362
NSAU 411
NGASU 817
NGMU 665
NGPU 214
NSTU 4610
НГУ 1992г
NSUE 499
NII 201
OmGTU 301
OmGUPS 230
СПбПК №4 115
PGUPS 2489
ПСПУ им. Короленко 296
ПНТУ им. Кондратюк 119
RANEPA 186
ROAT MIIT 608
RTA 243
RSHU 118
РГПУ им. Херцен 124
РГППУ 142
RSSU 162
"МАТИ" - РГТУ 121
РГУНиГ 260
REU ги. Плеханов 122
РГАТУ им. Соловьова 219
RyazGMU 125
RGRTU 666
SamGTU 130
СПбГАСУ 318
INGECON 328
СПбГИПСР 136
СПбГЛТУ им. Киров 227
СПбГМТУ 143
СПбГПМУ 147
SPbGPU 1598
СПбГТИ (ТУ) 292
СПбГТУРП 235
Държавен университет в Санкт Петербург 582
GUAP 524
СПбГУНИПТ 291
СПбГУПТД 438
СПбГУСЕ 226
СПбГУТ 193
СПГУТД 151
SPbGUEF 145
Електротехнически университет в Санкт Петербург "LETI" 380
ПИМаш 247
NRU ITMO 531
СГТУ им. Гагарина 114
СахСУ 278
SZTU 484
СибАГС 249
СибГАУ 462
СибГИУ 1655 г
СибГТУ 946
SGUPS 1513
СибГУТИ 2083
СибУПК 377
SFU 2423
SNAU 567
SSU 768
TRTU 149
ТОГУ 551
TGEU 325
TSU (Томск) 276
TSPU 181
ТулГУ 553
УкрГАЖТ 234
UlGTU 536
UIPCPRO 123
USPU 195
USTU-UPI 758
UGNTU 570
USTU 134
ХГАЕП 138
KhSAFC 110
HNAGH 407
HNUVD 512
KhNU им. Каразина 305
ХНУРЕ 324
KhNEU 495
Процесор 157
ЧитГУ 220
SUSU 306

Пълен списък на университетите

За да отпечатате файла, изтеглете го (във формат Word).