Работа със структури от данни в C и Python Част 10

Серия съдържание:
Това съдържание е част # от поредица # статии: Работа със структури от данни в C и Python
Това съдържание е част от поредицата: Работа със структури от данни в C и Python
Очаквайте нови статии от тази серия.
TRIE дървета
Изисква се да се изгради дърво от думите, включени в това изречение, но тези думи имат много повтарящи се знаци. TRIE дърво е проектирано да решава подобен проблем, както е показано на фигура 1.
Фигура 1. TRIE дърво
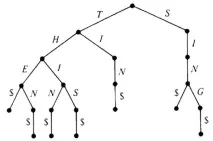

Символът$ в крайните възли на дървото екрайният маркер, който ще позволи на дървото да продължи с всички възможни комбинации от знаци. Показаното дърво е базирано на английската азбука, така че всеки възел може да има най-много 27 деца - 26 букви икраен маркер. На практика повечето възли ще имат по-малко от 27 деца.
TRIE дървото има своите предимства и недостатъци, тъй като изисква повече памет от двоичните дървета. В двоично дърво всеки възел може да има не повече от две деца, а в TRIE дърво изобщо няма ограничения за броя на децата, така че всичко зависи само от наличната памет и броя на символите в използваната азбука.
Списък 1 показва един възможен начин за дефиниране на основната структура на TRIE дърво.
Листинг 1. Основна структура за представяне на възли в TRIE дърво
В TRIE дърво листата се наричат TRIE_LEAF, а поддърветата се наричат TRIE_SUBTRIE. Следователно могат да бъдат дефинирани два типа възли, както е показано в листинги 2 и 3.
Листинг 2. Структура за описание на поддърво
Листинг 3. Структура за описаниевъзел
Листинг 4 предоставя структура за описание на самото TRIE дърво и функция за създаването му.
Листинг 4. Създаване на TRIE дърво
Изтриването на дърво се извършва с помощта на рекурсивна функция, която може да работи както с възли, които имат деца, така и с листови възли.
Списък 5. Функции за изтриване на възли в TRIE дърво
За решаването на този проблем е предложена дървовидна структура, при която височината на полученото дърво е съзнателно намалена. В B-дърво всеки възел може да има повече от две деца, така че дървото вече не е двоично дърво.
- m - ред (максимален брой дъщерни възли);
- всеки възел с изключение на корена трябва да има понеm/2 дъщерни възли;
- коренният възел има поне 2 дъщерни възела;
- всички листа са на едно ниво;
- възел, който имаk деца, може да имаk-1 ключове.
Що се отнася до ограничението на стойносттаm, то зависи от характеристиките на твърдия диск, по-специално от размера на неговия блок.
Всеки възел в B-дърво има подреден набор от ключове и набор от указатели към своите деца. Например, ако възелътn0 има три наследника -n1,n2,n3, тогава ключовете на възелаn0 трябва да бъдат два разделителя -a1 иa2, докато всички ключове на поддървотоn1 трябва да е по-малко отa1, всички ключове на поддървоn2 трябва да са по-малко отa2 и т.н.
B-дървото е балансирано дърво, така че всеки възел има две константи:
- U - максималният възможен брой дъщерни възли;
- L - минималният възможен брой дъщерни възли.
Когато се появи вмъкване илиизтриване на възел, тези константи се проверяват рекурсивно в цялото дърво отгоре надолу. Ако някой възел се отклони от стойноститеL иU, тогава възлите ще се слеят или разделят, за да възстановят баланса.
B-дърветата се използват широко в бази данни и файлови системи. Има и различни варианти на B-дървета, например 2-3 дърво, където всеки възел може да има не повече от три деца.
Фигура 2 показва пример за B-дърво. Когато броят на ключовете в даден възел надхвърли определен праг, тогава този възел се разделя на два възела, между които ключовете се разделят по равно. Всеки ключ във възел е коренът на поддърво, което съхранява ключове, които са в диапазона между съответните ключове на основния възел.
Фигура 2. B-дърво
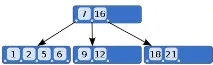

Тъй като B-дървото е балансирано, пътят от корена до всеки лист изисква същия брой стъпки. Съществува връзка между максималния брой ключове в един възел и максималния брой на неговите деца. Ако броят на ключовете е обозначен като2d, тогава броят на възлите обикновено ще бъде с още един -2d + 1. Съществува и връзка между височината на дървотоh и броя на ключоветеn.
В този тип дърво всички листа трябва да са разположени на едно и също ниво на дървото, така че такива дървета растат в посока на увеличаване на броя на дъщерните възли, а не на височина. Производителността на търсене в B-дърво зависи от размера на блока и скоростта на достъп до твърдия диск. Следователно, за да се увеличи ефективността на търсенето, е важно да се намали броят на възлите поради високото разклоняване на листата.
Има два вида B-дървета: B+ и B*. Фигура 3 показва B+-дърво. При тази реализация всички данни се съхраняват в отделен слой на дървото - в листа, докатоте са сортирани. Този слой може да бъде организиран в свързан списък, което е основната разлика от нормалното B-дърво.
Фигура 3. B+-дърво
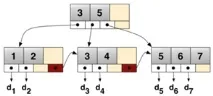

B* -дървото се използва във файловите системи HFS и Reiser4 и се различава отB+ -дърветата по това, че когато един възел е напълно запълнен с данни, той не се разделя на 2 възела. Вместо това се търси място във вече съществуващ съседен възел и едва след като и двата възела са запълнени, те се разделят на три възела.
Операции с B-дърво
Намирането или вмъкването на възел в такова дърво изисква само едно преминаване. Търсенето в B-дърво се различава от търсенето в обикновено двоично дърво по това, че в последния случай се основава на избора между десния и левия възел. В случай на B-дърво, това е линейно търсене между съседни ключове.
Когато вмъквате ключ, трябва да имате предвид няколко опции: ключът може да бъде добавен както към възел, така и към лист. В първия случай, ако възелът прелее, той се разделя наполовина. Фигура 4 показва как може да се формира B-дърво, когато в него последователно се вмъкнат естествени числа от 1 до 7. В този пример всеки възел може да съдържа не повече от два ключа.
Фигура 4. Създаване на B-дърво
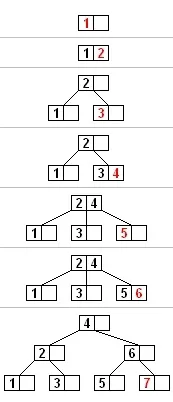
При премахване на ключ се получава подобен процес - сливане или разделяне на възли, което може да засегне цялото дърво от текущия възел до корена. Премахването може да се извърши и с едно преминаване, но трябва да се вземат предвид два сценария:
- ключът е разделителят;
- при изтриване на ключ, броят на ключовете може да стане по-малък от необходимия минимум.
Заключение
Това завършва цикъла, посветен на различни структури от данни. Обхваща основните формиорганизация на данните във връзка с два популярни езика за програмиране: C и Python.
Особено внимание беше отделено на свързаните списъци като една от най-важните и фундаментални структури. Ето как сравнихме ефективността на различни алгоритми за работа със свързани списъци.
Втората половина на цикъла беше посветена на също толкова важна структура от данни - дървета. Поради търсенето на дървета за файлови системи и бази данни, в тази област непрекъснато се провеждат различни изследвания и се предлагат нови подходи или оптимизирани версии на съществуващи алгоритми.
Изтегляне на ресурси
Свързани теми
- Работа със структури от данни в C и Python. Част 1.
- Работа със структури от данни в C и Python. Част 2.
- Работа със структури от данни в C и Python. Част 3
- Работа със структури от данни в C и Python. част 4
- Работа със структури от данни в C и Python. част 5
- Работа със структури от данни в C и Python. част 6
- Работа със структури от данни в C и Python. част 7
- Работа със структури от данни в C и Python. част 8
- Работа със структури от данни в C и Python. Част 9
- Работа със структури от данни в C и Python. част 10