Разклонени пукнатини

Разгледайте отново простия случай, когато стойността на R е постоянна. Този случай е показан на фиг. 6.6, а. Тук също се приема, че нарастването на пукнатината става при постоянно напрежение, т.е. интензивността на освобождаването на енергия зависи линейно от размера на пукнатината (ако не се вземат предвид корекциите за крайни размери и динамичните ефекти). В момента, когато размерът на пукнатината е два пъти по-голям от първоначалния размер, при който възниква нестабилност (A) (т.е. когато Δ a \u003d a c), скоростта на освобождаване на енергия е два пъти (B) устойчивостта на растеж на пукнатината R. Теоретично това означава, че се отделя достатъчно енергия, за да се развият две пукнатини. В резултат на това може да се получи разклоняване на пукнатината. При по-нататъшно нарастване на пукнатината до размера a = 3a c (Δ a = 2 a c ), интензитетът на отделяне на енергия G става равен на 3 R . Това означава, че три пукнатини могат да растат едновременно, т.е. могат да възникнат множество разклонения.

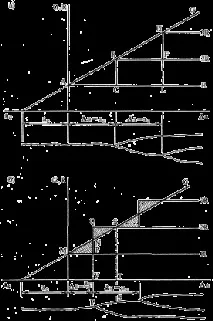
Ориз. 6.6. Бифуркация на пукнатината: a - без отчитане на кинетичната енергия; б - отчитане на кинетичната енергия

Съгласно фиг. 6.6 може да възникне бифуркация, ако a/a c = 2; 3 и т.н. Използвайки уравнение (6.10.), може да се покаже, че минималната скорост на разпространение на пукнатината, необходима за разклоняване, е 0,19v s (първото разклонение възниква при c / a = 0,5). Разклоняването влияе върху скоростта на разпространение на пукнатини. В момента на разклоняване нарастването на кинетичната енергия рязко се забавя и става равно на площите на триъгълниците ABC и BHF, а не на AHL (фиг. 6.6, а). Това означава, че раздвоените пукнатини трябва да се движат по-бавно от единичните. Това също означава, че уравненията, получени в тази глава, са валидни само при липса на разклонения.

Наличието на кинетична енергия може да доведе до разклоняване дори при повечениска скорост, както е показано на фиг. 6.6b. Общото количество кинетична енергия, което е налично в момента, когато размерът на пукнатината се е увеличил с Δ a = a c /2, е показано на фиг. 6.6b триъгълник MNP . Тази кинетична енергия може да се използва за разпространение на пукнатината. Да приемем, че има разклонение, когато Δ a = a c /2 и когато енергията, необходима за разпространение на пукнатина, се получава чрез преобразуване на кинетичната енергия MNP. Ако пукнатината се раздвоява, тогава енергията, необходима на двете пукнатини да изминат разстоянието Δ a е равна на 2 R . Нека двата клона се движат от P към S. Общата консумация на енергия е равна на площта на четириъгълника QSTV. Само част от тази енергия може да бъде получена поради освобождаването на енергия на еластична деформация, а именно енергията, равна на площта NSTV, а останалата част QSN в момента на разклоняване вече е налична под формата на кинетична енергия MNP. По време на по-нататъшното нарастване на пукнатината консумацията на енергия надвишава G . Няма приток на енергия, който да я преобразува в кинетична енергия, докато наличната кинетична енергия вече е отишла за разпространение на пукнатини. След като размерът на пукнатината допълнително се увеличи с c /2, кинетичната енергия ще бъде напълно изразходвана за разпространение на клона на пукнатината (област MNP = NQS). Нулевата кинетична енергия съответства на нулева скорост на пукнатината, т.е. скоростта на разпространение на пукнатината постепенно намалява до нула в точка S. Тъй като интензивността на освобождаването на енергия от еластични деформации все още е достатъчна за растежа на две пукнатини, процесът на разпространение на пукнатини не спира напълно: възниква нестабилност, след което процесът на разпространение на бифуркирана пукнатина се възобновява с нарастваща скорост. По същия начин може да се случипо-нататъшно разклоняване.

Механизмът за разклоняване, показан на фиг. 6.6, b, също може да работи, ако размерът на пукнатината се увеличи с Δ a по-малко от a c /2, както е показано на фиг. 6.7. След като пукнатината измине известно разстояние, кинетичната енергия ще бъде равна на площта TXV. Тази кинетична енергия може да се използва за образуване и отглеждане на нов клон. За кратък период от време тази кинетична енергия се изразходва напълно (площта TXV е равна на площта XZAB). Това означава, че скоростта на разпространение на двете пукнатини става равна на нула. Скоростта на освобождаване на енергия от еластични деформации е недостатъчна (точка B ), за да поддържа разпространението на двете пукнатини, но е повече от достатъчна за растежа на една от тях. Това означава, че един от клоните отново става нестабилен и продължава да се разпространява, докато другият напълно спира да расте. След известно време може да се появи друго разклонение по абсолютно същия начин (точка F). (Малко вероятно е първият клон да започне да расте отново: той се намира зад фронта на основната пукнатина, където напреженията вече са намалели до известна степен.) След като кинетичната енергия стане равна на площта на BCDF, тя може да премине към образуването на втория клон (HFML).

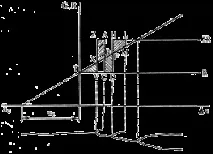
Ориз. 6.7. Неразмножаващи се клони

В практиката понякога се наблюдава разклоняване на пукнатини, особено когато пукнатините се образуват в резултат на разцепване и се разпространяват с висока скорост. Разклоняването на пукнатини в счупено стъкло на прозорец е добре известно (в този случай проблемът донякъде се усложнява от наличието на вътрешни напрежения в стъклото). В случай на експлозия на съд под високо налягане, в резултат на разклоняване на пукнатини, те могат да се разпаднат на много части. Последното се случва с повечевероятност, ако стойността на G продължава да расте по време на разрушаване, т.е. в пълни с газ контейнери (в които налягането не намалява веднага след образуването на пукнатини). На фиг. 6.8 показва пример за бифуркация на пукнатина.

Все още има много несигурност относно скоростта на разпространение на пукнатината, необходима за нейното разклоняване. Измерените скорости на разклоняване не съвпадат с резултатите от теоретичните изчисления. Ако се получи разклоняване без изразходване на кинетична енергия, тогава необходимата скорост за това трябва да бъде от порядъка на 0,19ν s, както беше показано по-рано. Ако кинетичната енергия може да се използва за разпространение на пукнатината, тогава разклоненията могат да възникнат при по-ниски скорости. За да може раздвоената пукнатина да продължи да се разпространява, както е показано на фиг. 6.6, b, минималното увеличение на размера на пукнатината трябва да бъде равно на Δ a \u003d a c / 2 или a c / a \u003d 0,66. В този случай минималната скорост, при която възниква разклоняване, получена от уравнение (6.10), е. 6.7. Други несъответствия между теорията и експеримента несъмнено възникват поради влиянието на динамиката върху стойностите на G и R, което беше обсъдено в предишните параграфи на главата. В допълнение, всички наши разсъждения се основават на предположението, че напрежението е постоянна стойност, т.е. G нараства пропорционално на размера на пукнатината съгласно закона G = πσ 2 a / E. Въпреки това, при фиксирани захващания напрежението намалява по време на разпространението на пукнатината, тъй като общата твърдост на пробата е толкова по-ниска, колкото по-дълга е пукнатината. В резултат на това стойността на G нараства по-бавно, отколкото е пропорционално на размера на пукнатината, а за определена геометрия на пробата може дори да намалее. Това явлениекоето се обсъжда в следващия параграф, води до промени на фиг. 6.6 и 6.7, но не променя основните принципи.

Ъгълът между разклоненията на пукнатината може да бъде предвиден доста точно (вижте [18]), като се вземе предвид растежът на пукнатина от смесен тип. Ако пукнатината се отклонява от равнината, перпендикулярна на посоката на напрежението на опън, тогава тя също е подложена на действието на срязващи напрежения, т.е. K II ≠ 0. Поведението на пукнатината при комбинирано действие на K I и K II е изследвано в гл. XIV. Тази глава показва, че ъгълът между клоните трябва да бъде от порядъка на 15°, което се съгласува добре с това, което се случва в действителност.

Ориз. 6.8. Сенчести снимки на процеса на разклоняване на пукнатината в стъклена плоча [широчина на плочата 100 mm, дължина 300 mm, дебелина 9 mm; натоварването, при което възниква счупването, е 310 kgf; времето на експозиция на един кадър е 4 µs (според Kalthoff и Института по механика на твърдото тяло)]