Риск, несигурност и ограничения за вземане на решения, парите никога не спят
Парите като инструмент на свободата
Риск, несигурност и граници на решения

Риск и несигурност. В търсене на смисъл
Кардиналните промени в разбирането на риска и несигурността са свързани с два фундаментални труда - „Риск, несигурност и печалба” на американския икономист Ф.Х. Найт (Риск, несигурност и печалба, 1921 г.) и Теория на спекулациите от френския математик Луи Башелие (Теория на спекулациите, 1900 г.).
Ф.Х. Найт, въз основа на анализа на печалбата, съвършената и несъвършената конкуренция, стигна до определението за риск и несигурност. Според Найт несигурността е състояние на средата, при което класификацията на отделните случаи не подлежи на никаква систематизация, а рискът е когато такава систематизация е възможна и позволява оценка на вероятността и последствията от неблагоприятни събития. Найт свързва състоянието на риск/несигурност с условията на съвършена/несъвършена конкуренция [2]. Както ще видим по-късно, констатациите на Найт са далеч пред времето си и се доближават до задачата за справяне с несигурността и управление на риска.
Ако Найт се опита да получи представа за риска от анализ на общите икономически условия, тогава Луис Башелие стигна до дефинирането на риска от конкретен - чрез математическо изследване на проблема за случайното разпределение на пазарните цени. Трудно е да си представим по-добър пример за риск от отклонението на пазарните цени от очакваната средна стойност. Пазарните цени изглеждат напълно хаотични и непредвидими. Заслугата на Bachelier се състои в това, че той идентифицира модел в промяната на пазарните цени и показа, че те са обект на универсалния модел на нормално разпределение, който е известен също като камбановата крива на Гаус [3]. Да разбере каквопредставлява този модел, помислете за прост пример - вероятностното разпределение на стойностите на 6-странен зар за игра. Ако хвърлим 1 зар, тогава вероятността да получим стойността на числото "3" ще бъде 1/6 или 16,67% - както всяко друго. Ако считаме загубата на стойност "3" за печалба, тогава вероятността за печалба ще бъде 16,67%, а загубата съответно 83,33%. Въпреки това, ако вземете няколко куба, тогава вероятностното разпределение на стойностите ще бъде подложено на напълно различен модел - камбановидната крива на Гаус. Оказва се, че вероятността да се получи средната стойност ще бъде много по-висока от екстремните стойности. И колкото повече кубчета използвате, толкова повече разпределението на вероятностите ще се доближава до разпределението на Гаус, т.е. вероятността да се получи средната стойност ще бъде по-висока от екстремните.
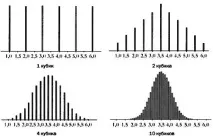
Класическото разпределение на Гаус гласи, че вероятността за едно стандартно отклонение от средната стойност е 68%, две - 94%, три - 98%. С други думи, вероятността за значително (повече от 3) отклонение от средната стойност е по-малко от 2% (вижте фиг.)
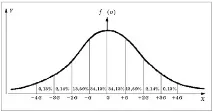
От кривата на Гаус до теорията на портфолиото на Марковиц
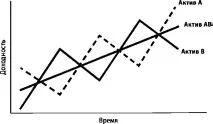
Така G. Markowitz беше първият, който приложи модела, идентифициран от Bachelier (ниска степен на отклонение на случайно разпределение от определен среден диапазон), за да реши специфичен проблем за намаляване (управление) на риска. Тестването на модела на инвестиционния портфейл на Марковиц върху голяма извадка от статистически данни показа, че портфейл, съставен от отрицателно корелирани активи, наистина намалява пазарния риск до известна степен (вижте Фиг.)
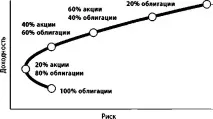
Идеите на Г. Марковиц са доразвити в трудовете на други математици и икономисти (Тобин, Линтнер, Шарп, Милър)и с течение на времето се оформи в научна система, наречена модерна портфолио теория. Логичното заключение на теорията за портфейла беше развитието на хипотезата за ефективния пазар, според която пазарните цени винаги точно и пълно отразяват цялата налична информация за дейността на компаниите, така че анализът на отделни ценни книжа не може да даде конкурентно предимство на отделен участник на пазара. Тази хипотеза е формулирана през 1972 г. от Ю. Фама [5]. За обективност трябва да се отбележи, че портфейлната теория не беше веднага призната от професионалната инвестиционна общност. Едва след като значението на тези произведения беше признато от Нобеловия комитет (през 1990 г. Марковиц, Милър и Шарп бяха удостоени с Нобелова награда), тази концепция започна активно да се прилага на практика. Оттогава портфейлната теория се превърна в основен работен инструмент на пенсионните фондове, управляващите дружества и други институционални инвеститори.
Критика на портфолио теорията. Бъфет, Талеб, Манделброт
Н. Талеб в книгата си „Черният лебед. Под знака на непредсказуемостта” [7] заключава, че математическите модели на отклонение от очакваната стойност работят само в случаите, когато играта има ясни правила и проста механика за определяне на печелившата страна, което фондовият пазар, който се влияе от множество фактори, не е („заблуда на играта”). Талеб описва две взаимно изключващи се системи, в едната от които математическите модели работят, а във втората не. Първият той нарича „среден стан” (система, подчинена на разпределението на Гаус), вторият „екстремален стан” (система, която позволява значителни отклонения от средната стойност) [8].
Несигурност и риск в теорията на игрите
Естествено не природата плаща, анякаква трета страна (или набор от страни, които влияят върху вземането на решения от играча и са обединени в понятието „природа“). Възможен е и друг начин за конкретизиране на матрицата на играта с природата - под формата на т. нар. матрица на риска или матрица на пропуснатите възможности. В този случай рискът на играча при използване на всяка конкретна стратегия за всяко конкретно състояние на средата се определя като разликата между печалбата, която играчът би получил, ако предположението му за най-вероятното състояние на средата се окаже вярно, и печалбата, която би получил, ако сгреши. В резултат на това оптималната стратегия ще бъде тази, при която играчът получава максимална печалба.
За вземане на решения в условията на несигурност се използват други методи за вземане на решения. „Най-мекият“ случай на игра с природата в условия на несигурност са игрите на „доброкачествена“ или стохастична несигурност, когато знаем вероятностите за проявление на природните състояния - тогава решенията обикновено се вземат въз основа на критерия за максимална очаквана средна печалба или минимален очакван среден риск. Тези проблеми са добре решени с помощта на статистическите игри на Валд. За визуализиране на информация, при решаване на проблеми, възможните стратегии често се рисуват под формата на дърво на решенията (вижте фигурата).
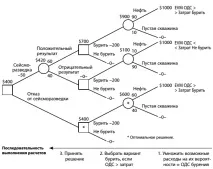
Ситуацията е по-сложна при вземането на решения в условия на пълна несигурност, свързана с липсата на информация за вероятностите за състоянието на околната среда (природата), което в теорията на игрите се нарича "безнадеждно" или "лошо". В такива случаи се използват методи (критерии) на maximax, Wald, Savage, Hurwitz и Bayes-Laplace за определяне на най-добрите решения. Тези методи позволяват да се получи оптимална стратегия в зависимост от субективното отношение на играча към вероятността за успехрезултат от събитията. Така че, когато се прилага критерият maximax, се признава най-доброто решение, при което се постига максимална печалба, поради което този критерий често се нарича критерий за екстремен оптимизъм. Максиминният критерий на Валд разглежда природата като агресивен и съзнателно действащ противник от типа, който се противопоставя на играча в стратегически игри. В резултат на това при прилагането на този критерий от всички най-неуспешни резултати се избира най-добрият. Това е позиция на безопасно убежище на краен песимизъм, предназначена за най-лошия случай. При прилагането на минимаксния риск метод на Savage изборът на стратегия е подобен на избора на стратегия по принципа на Wald, с тази разлика, че играчът се ръководи не от матрицата на изплащане, а от матрицата на риска. Критерият за песимизъм-оптимизъм на Хурвиц при избора на решение препоръчва да се ръководи от някакъв среден резултат, характеризиращ състоянието между краен песимизъм и необуздан оптимизъм.
Решаването на проблеми за определяне на оптималната стратегия при несигурност разкри друг проблем - когато прилагаме повечето от горните методи, ние изхождаме от предположението, че играчът всеки път ще избира стратегията, която му позволява да получи най-голяма печалба. Благодарение на трудовете на J. Neumann и O. Morgenstern в теорията на игрите беше въведена дефиницията на функцията на полезност, което направи възможно съпоставянето на очакваната печалба като обективен компонент на играта със склонността на играча към риск като негов субективен компонент. Това допълнително разшири възможностите на теорията на игрите за преодоляване на несигурността и управление на риска.
По този начин, при липса на информация за вероятностите за състоянието на околната среда, теорията на игрите не дава недвусмислени и математически строги препоръки за избор на критерии за вземане на решение. Товадо голяма степен се дължи не на слабостта на теорията на игрите, а на несигурността на самата ситуация. Единственият разумен изход в такива случаи е да се опитате да получите допълнителна информация, например чрез изследване или експерименти. При липса на допълнителна информация взетите решения са теоретично недостатъчно обосновани и до голяма степен субективни. Въпреки че използването на математически методи в игрите с природата не дава абсолютно надежден резултат, а последният е субективен до известна степен (поради производството на избора на критерия за вземане на решения), това е създадено от „Околна среда“. Подобно рационализиране на идеите за проблема само по себе си допринася за подобряване на качеството на взетите решения [10].
Обобщаване
Икономиката е натрупала достатъчно начини за управление на риска в идеални системи, както и доказателства, че всички модели се провалят, когато условията вече не са идеални. Идеалните системи трябва да отговарят на следните условия: равномерно разпределение на надеждна информация между всички участници в системата, рационални мотиви на участниците в системата, ясни и непроменливи правила на взаимодействие, стабилност на други външни и вътрешни фактори.
Следващият въпрос, на който трябва да отговорим, е доколко принципно може да се преодолее несигурността. Един от начините за управление на несигурността, а именно създаването на идеални условия, когато математическите методи започват да работят, ние вече анализирахме. Виждаме тованауката, представена от теорията на игрите, се доближи до проблема за определяне на оптималната стратегия в условия на пълна несигурност. Любознателният научен ум обаче се противопоставя на фундаменталните закони на Вселената, като например принципа на неопределеността на Хайзенберг, според който е невъзможно да се измери точно състоянието на квантовите частици, тъй като по време на измерването на един компонент вторият вече ще се промени толкова много, че измерването на първия престава да има смисъл. Добрата новина е, че съвременната наука е разработила достатъчен брой начини за преодоляване на несигурността и управление на рисковете, така че участниците в икономическите взаимоотношения да могат значително да подобрят качеството на своите решения.
Изводи
1) Рискът е частен случай на по-широко понятие за несигурност. Концепцията за риск е приложима само за онези системи, които са подчинени на определени условия (идеални системи). Във всички останали случаи е по-правилно да се говори за несигурност
2) Математическите модели добре описват и измерват риска по отношение на идеални системи, стига да се запази условието за тяхната идеалност. Отвъд идеалните системи започва зона на несигурност.
3) Вземането на решения в условия на несигурност започва с факта, че трябва да приемете идеята, че несигурността е непреодолима по принцип, но по-специално способността да я управлявате. Това означава, че разбирате при какви условия можете да действате с по-голяма увереност в благоприятния изход от събитията и при какви условия е по-добре изобщо да се въздържате от вземане на активни решения.
4) Като цяло управлението на несигурността и риска се свежда до три основни парадигми - приемане на фундаменталната непреодолима несигурност, делегиране на несигурност, овладяване наизбор на моменти на несигурност и управление на риска. Най-добрите стратегии за управление включват и трите компонента, а най-лошите - само един.
Използвани източници
1 - Княгинина Г.В. Еволюция на подходите към дефинирането на понятията "несигурност" и "риск". Списание "Нов университет". Поредица "Икономика и право". - 2011. - № 3 (виж тук)
2 — Найт Ф. Х. Риск, несигурност и печалба / пер. от английски. - М .: Дело, 2003. - 360 с.
3 - Л. Башелие. Теория на спекулациите. Annales scienctifiques de l`E.N.S., 3-eme serie, том 17 (1990), p. 21-86. Превод на български - вижте тук.
4 - Марковиц Хари М. Избор на портфолио // Journal of Finance. 1952. № 1 стр. 71-91
5 - Фама Е.Ф. Ефективни капиталови пазари: Преглед на теорията и емпиричната работа // Journal of Finance. 1970 г.
6 - Есе за инвестиции, корпоративни финанси и управление на компании / Уорън Бъфет. пер. от английски. - M .: Alpina Business Books, 2005. - S. 94
7 - Талеб, Насим Никълъс. Черният лебед: Въздействието на силно невероятното. - Ню Йорк: Random House, 2007 г.
8 - Н. Талеб. "Черният лебед. Под знака на непредсказуемостта. Резюме от S.V. Багузина - вижте тук
9 - Б. Манделброт. „(Не)послушни пазари: фрактална революция във финансите. Резюме от S.V. Багузина - вижте тук
10 - Моделиране на рискови ситуации в икономиката и бизнеса: учеб. надбавка / А.М. Дубров, Б.А. Лагоша, Е.Ю. Хрусталев; Изд. Б.А. Лагоши - М .: Финанси и статистика, 2000. - 176 с.