Ръководство за потребителя на Mathcad
Също така е възможно елементите на вектора да бъдат представени графично. Такава графика е показана на фигура 4. За да я създадете, направете следното:
- Дефинирайте дискретна променливаi, която е долният индекс на всеки елемент, който трябва да бъде изчертан.
- Дефинирайте вектор yi. Използвайте клавиша с лява скоба [ , за да създадете долен индекс.
- Натиснете @, за да създадете шаблон на диаграма.
- Поставете средната кутия на вертикалната ос иiв средната кутия на хоризонталната ос.
- Натиснете[F9], за да видите графиката.
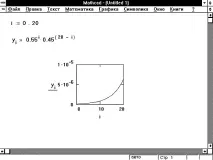
Фигура 4: Графично представяне на вектор.
Долните индекси трябва да са неотрицателни цели числа (или цели числа, по-големи или равни на ORIGIN, ако ORIGIN е 0.) Това означава, че абсцисата може да приема само цели числа. Ако искате да използвате дробни или отрицателни стойности на оста x, начертайте функцията, както е на фигура 2, или начертайте един вектор срещу друг, както е описано в следващия раздел.
Ако имате набор от данни, който няма подходяща функционална връзка, както е на фигура 4, но е твърде малък, за да използвате файлове с данни, можете да използвате входна таблица, за да създадете вектор.
Картографиране на един вектор спрямо друг
Фигура 5 показва как да се покаже един вектор във връзка с друг. Не е необходимо векторите да са с еднаква дължина. Изисква се само:
- И двата вектора трябва да споделят един и същ индекс. Например, не можете да начертаете xi спрямо yj, защотоiиjса различни индекси.
- Всяка стойност на долен индекс трябва да съответства на някакъв елемент във всеки вектор. Например, акоxима само два елемента, аyима осем елемента и дискретната променливапромени от 0 на 7, ще се покаже съобщение за грешка„индекс извън границите“.
За да създадете графиката, показана на фигура 5, направете следното:
- Дефинирайте дискретна променливаi, която е долният индекс на всеки екранен елемент.
- Дефинирайте масивите xi и yj. Използвайте клавиша с лява скоба [, за да напишете индекс.
- Натиснете @, за да създадете шаблон на диаграма.
- Поставете yi в средното поле на оста y и xi в средното поле на оста x.
- Натиснете[F9], за да видите графиката.
Въпреки че векторътxна фигура 5 представлява набор от равномерно разпределени стойности, това не е необходимо. Изисква се само индексътiда бъде равномерно разположени цели числа. Няма такова ограничение за xi. Това позволява да се използват не само цели числа по оста x и в същото време да се задоволи изискването за целочислени индекси. На фигура 5 yi се изчислява директно по отношение на xi. Би било възможно да се изчислятxиyнезависимо от третата променлива. Ако само два вектора използват една и съща дискретна променлива, можете да ги покажете на една и съща графика.
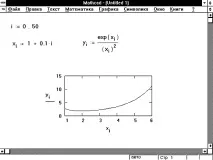
Фигура 5: Съвместно графично представяне на два вектора.

Фигура 6: Два вектора, изчислени независимо.
Фигура 6 показва диаграма в полярни координати, в която кактоx, така иyзависят от променливитеrи q. Фигура 6 използва вектори за решаване на същия проблем, който беше решен с помощта на функциите на Фигура 3.
Обърнете внимание, че на фигура 6 дискретната променливаiтрябва да приема цели числа и се използва за дефиниране на вектор q от равномерно разположени нецели числа. Фигура 3q беше дефинирано директно като дискретна променлива. Това беше възможно, защото функциите не изискват цели аргументи, както векторите изискват целочислени индекси.
Графично представяне на файлове с данни
Например, ето как да покажете данни от електронна таблица:
- Запазете електронната таблица като ASCII текстов файл с разширение.prn.
- Използвайте функциятаREADPRN, за да импортирате файла.prn в Mathcad като матрица. Вижте подраздел „Четене на матрица с помощта на функциятаREADPRN“ .
- Фигура 7 показва процеса на графично представяне на вектори от данни, импортирани от файл.prn.

Фигура 7: Графично представяне на импортирани вектори
Графично представяне на други изрази
Фигури 2-6 показват някои от най-често срещаните типове диаграми. Друг пример на фигура 12 показва начертаването на константа, използвана като риск, върху графиката на друга функция. Възможните графики не се ограничават до тези примери. Можете да начертаете всеки набор от точки, чиито координати се изчисляват от всяка двойка изрази, стига тези изрази да използват едни и същи дискретни аргументи.