Събиране на числа с различни знаци, математика-повторение
Събиране на отрицателни числа.
Сумата от отрицателните числа е отрицателно число. Модулът на сбора е равен на сбора от модулите на членовете.
Нека видим защо сумата от отрицателните числа също ще бъде отрицателно число. За това ще ни помогне координатната линия, на която ще извършим събирането на числата -3 и -5. Нека отбележим точка на координатната права, съответстваща на числото -3.
Към числото -3 трябва да добавим числото -5. Къде отиваме от точката, съответстваща на числото -3? Точно така, наляво! За 5 единични сегмента. Маркираме точката и записваме съответстващото й число. Това число е -8.

Така че, когато добавяме отрицателни числа с помощта на координатна линия, ние винаги сме вляво от референтната точка, следователно е ясно, че резултатът от добавянето на отрицателни числа също е отрицателно число.
Забележка. Добавихме числата -3 и -5, т.е. намери стойността на израза -3+(-5). Обикновено, когато добавят рационални числа, те просто записват тези числа с техните знаци, сякаш изброяват всички числа, които трябва да бъдат добавени. Такава нотация се нарича алгебрична сума. Приложете (в нашия пример) запис: -3-5=-8.
Пример. Намерете сбора на отрицателните числа: -23-42-54. (Съгласете се, че този запис е по-кратък и по-удобен като този: -23+(-42)+(-54))?
Решаваме по правилото за събиране на отрицателни числа: събираме модулите на членовете: 23+42+54=119. Резултатът ще бъде със знак минус.
Обикновено го записват така: -23-42-54 \u003d -119.
Събиране на числа с различни знаци.
Сборът от две числа с различни знаци има знак на събираемото с голям модул. За да намерите модула на сумата, трябва да извадите по-малкия модул от по-големия модул.
Нека да извършим добавяне на числа с различни знаци с помощта на координатната линия.
1) -4+6. Изисква дадобавете числото -4 към числото 6. Отбележете числото -4 с точка на координатната линия. Числото 6 е положително, което означава, че от точката с координата -4 трябва да отидем надясно с 6 единични отсечки. Завършихме вдясно от началото (от нула) с 2 единични сегмента.
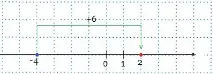
Резултатът от сбора на числата -4 и 6 е положителното число 2:
— 4+6=2. Как можахте да получите номер 2? Извадете 4 от 6, т.е. извадете по-малкото от по-голямото. Резултатът има същия знак като члена с голям модул.
2) Изчислете: -7+3, като използвате координатната линия. Отбелязваме точката, съответстваща на числото -7. Отиваме надясно с 3 единични отсечки и получаваме точка с координата -4. Бяхме и останахме вляво от началото: отговорът е отрицателно число.

— 7+3=-4. Можем да получим този резултат по следния начин: извадихме по-малкия от по-големия модул, т.е. 7-3=4. В резултат на това беше зададен знакът на термина с по-голям модул: -7 > 3.
Примери. Изчислете:a) -4+5-9+2-6-3;b) -10-20+15-25.
Решение.a) първо добавете всички отрицателни числа (-4-9-6-3=-22), след това всички положителни числа (5+2=7) и след това добавете числа с различни знаци (-22+7=-15). Записваме го така:
b) -10-20+15-25=-55+15=-40.