Шифрова блокова верига
(CBC) Верижно свързване на шифрови блокове Верижното шифроване на блокове е една от схемите за симетрично криптиране, използващи обратна връзка. Всеки блок с обикновен текст (с изключение на първия) се добавя по модул 2 (XOR) бит по бит към резултата от предишното криптиране. Когато шифровате първия блок, векторът за инициализация (IV) се използва като предходен блок, който се съгласува между подателя и получателя преди започване на процеса на шифроване/декриптиране.
Има редица различни модификации:
- (BC) блокова верига
- (CBC$) Cipher Block Chaining с произволен IV (инициализиращ вектор)
- (CBCC) шифрова блокова верига с контролна сума
- (PCBC) верижно свързване на шифрови блокове
- (CBCPD) шифрова блокова верига на разликата в обикновен текст
Постановка на проблема за защита на информацията (предизвикателство за сигурността)
Основната характеристика на тази схема за криптиране е, че за разлика от схемата ECB, едни и същи блокове с обикновен текст, принадлежащи към едно и също съобщение, се криптират в различни блокове с шифрован текст, така че отделни модели в блока не се съхраняват.
Тази схема за криптиране има следните характеристики:
- Ако някой бит от шифрования текст бъде променен по време на предаване на съобщението, грешката ще се разпространи към текущия и следващия блок от данни в обикновен текст. Грешката обаче няма да се разпространи в следващите блокове (след един), следователно CBC схемата се нарича още самолечение.
- В случай на загуба или вмъкване на поне един бит в шифрования текст,отместване на битове и граници на блокове, което ще доведе до погрешно дешифриране на всички следващи блокове с шифрован текст (коригируемо, когато се прилагат методи за контрол на границите на блок с шифрован текст)
- Нападателят може да добави блокове в края на криптираното съобщение, като по този начин допълва обикновения текст (но без ключ се оказва боклук)
- Две идентични съобщения имат еднакви шифровани текстове, когато използват един и същ вектор за инициализация (IV).
- От параграф 4 следва, че ако един вектор за инициализация (IV) се използва за криптиране на различни съобщения, които имат едни и същи първи k блока, първите k блока на шифрования текст също ще бъдат еднакви, което прави възможно извършването на атака (описано в раздела за проблеми със сигурността на схемата на ЕЦБ)
- Обобщавайки точки 5 и 4, можем да кажем, че за много големи съобщения (32 GB с дължина на блока 64 бита) все още е възможно да се използват атаки, базирани на структурните характеристики на обикновения текст (последствие от парадокса на рождения ден).
- IV грешка във времето е фатална за работния процес
- Грешка от поне един бит по време на криптиране води до грешки във всички следващи блокове на шифрования текст - в резултат пълен боклук с правилно декриптиране
- Процесът на дешифриране може да се извърши паралелно.
Теоретични основи на решаването на проблеми (теоретични въпроси)
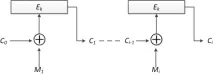
Математически една симетрична схема за криптиране може да бъде описана по следния начин:
Шифроване:
Дешифриране:
където е откритият текст, са N-битовите блокове на отворения текст, t е броят на блоковете, на които е разделен отвореният текст, са блоковете с шифрован текст, съответстващи на блоковете с отворен текст, и са алгоритмите за криптиране и декриптиране на ключ k,IVе векторът за инициализация.
Нека докажем товакриптирането и дешифрирането водят до един обикновен текст:
CBC CTS (CipherText Stealing) улавяне на шифрован текст
Последният блок с обикновен текст (с номер t) може да съдържа по-малко от N бита, в който случай трябва да бъде подплатен, което не винаги е възможно - в този случай се използва техниката за улавяне на шифрован текст CBC CTS (CipherText Stealing), която позволява използването на схемата CBC без подпълване на обикновения текст до множество от N бита (подобно на ECB CTS).
В тази схема последните два блока с обикновен текст Mt и Mt-1 са криптирани отделно по различен начин и в различен ред. Да предположим, че Mt-1 има N бита и Mt има n бита, с n криптографски примитиви и/или протоколи
Практически приложения на криптографски структури, характеристики на тяхното прилагане (Практически въпроси)
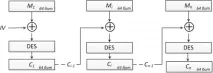
Схемата за симетрично криптиране CBC често се използва за криптиране на съобщение. Паралелната обработка обаче не е възможна поради естеството на работата, тъй като се използва верижният механизъм. По същата причина схемата CBC не се използва при криптиране на масиви от файлове с произволен достъп (бази данни. Доста често схемата CBC се използва за удостоверяване на съобщение (подпис).
Нека разгледаме по-подробно работата на алгоритъма DES, използвайки схемата за криптиране CBC:
изходният файл M, съгласно схемата CBC, е разделен на блокове от 8 байта (64 бита). Всеки от тези блокове с обикновен текст се добавя по модул 2 (операция XOR) към резултата от криптиране на предишния 64-битов блок с обикновен текст. Първият блок от обикновен текст се добавя към началния IV. След това получената сума се криптира с помощта на алгоритъма DES с помощта на ключ, койтоизвестни както на подателя, така и на получателя. Полученият 64-битов блок от шифрован текст се добавя по модул 2 към следващия блок от обикновен текст
Терминологичен речник
Библиографски указател (Библиография)
- (ECB) Електронна кодова книга
- (ECB CTS) Кражба на CipherText
- ( CBC) Верижно свързване на шифрови блокове Верижно шифроване на блокове
- (CBC CTS) Кражба на CipherText
- (BC) блокова верига
- (CBC$) Cipher Block Chaining с произволен IV (инициализиращ вектор)
- (CBCC) шифрова блокова верига с контролна сума
- (PCBC) верижно свързване на шифрови блокове
- (CBCPD) шифрова блокова верига на разликата в обикновен текст